Binomialverteilung

Bei vielen Experimenten enthält der Ergebnisraum nur 2 mögliche Ausfälle, die sich gegenseitig ausschließen: Kindergeburt (Junge oder Mädchen) , Lotterie (Niete oder Treffer), Einsatz Medikament (Heilung oder keine Heilung), Fabrikationskontrolle (brauchbare, unbrauchbare Ware), ....... . Sind solche Experimente wiederholbar, ohne, dass sich die Wahrscheinlichkeit für das Eintreffen der beiden Teilergebnisse sich ändert , dann spricht man von Bernoulli-Experimenten, bei n-maliger Durchführung mit gleicher Trefferwahrscheinlichkeit spricht man von einer Bernoulli-Kette der Länge n (Zufallsexperiment: Ziehen mit Zurücklegen).

Sehen wir uns zunächst mal ein Mini-Galton-Brett an: (Auf einer Seite der Uni Konstanz findest Du eine Simulation dazu.)



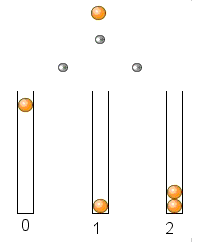
Kugeln treffen auf eine regelmaßige Anordnung von Hindernissen und prallen von dort ab: Mit der Wahrscheinlichkeit p fallen sie dann nach rechts, mit der Wahrscheinlichkeit q=1-p nach links.
Wir fragen uns, mit welcher Wahrscheinlichkeit eine Kugel in Behälter 0, in Behälter 1 und in Behälter 2 trifft (2-stufige Kette).

Denkt man sich das zugehörige Baumdiagramm dazu gezeichnet und wendet die entsprechenden Pfadregeln an, dann erkennt man sofort, dass
P(0)= q²,
P(1)=qp+qp=2qp und
P(2)=p² ...(und schon taucht in unserem Geist die Erinnerung an die Ähnlichkeit mit der 1. binomischen Formel (a+b)² = a² +2ab + b² auf mit den Koeffizienten 1,2,1. ...Oder ???).

Vergößern wir unser Galton-Brett und betrachten die Bernoulli-Kette der Länge 3:



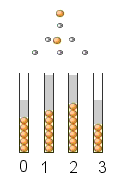
Wieder stellen wir uns das zugehörige Baumdiagramm vor und erhalten:

P(0)= q³
P(1)=3 q²p¹
P(2)=3 q¹p²
P(3)=p³ .... (und an dieser Stelle sollte die Erinnerung an das Pascal'sche Dreieck und den Binomialkoeffizienten auftauchen.)



Es gilt also:



Zur Überprüfung Deiner Vermutung vergrößere das Galton-Brett weiter:



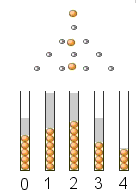
und



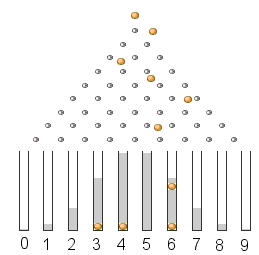
Die zugehörigen Baumdiagramme mit ihren Regeln bleiben Dir überlassen.

Zusammenfassung:

Satz über die Trefferwahrscheinlichkeit: Wir betrachten eine n-stufige Bernoullikette mit der Grundwahrscheinlichkeit p und der Gegenwahrscheinlichkeit q=1-p. Für einen Treffer auf Platz k gilt



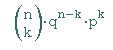
Information:

Man nennt die Zufallsgröße X binomialverteilt: Satz: Bei einer n-stufigen Bernoulli-Kette mit der Grundwahrscheinlichkeit p und der Gegenwahrscheinlichket q = 1 - p für genau k Treffer (0 kleiner gleich k kleiner gleich n):

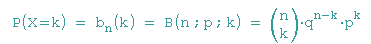
Erwarungswert und Varianz bei Bernoulli-Ketten:

Setzt man in die allgemeine Formel für den Erwartungswert einer Zufallsvariablen X



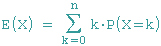
die Formel für die binomialverteilte Zufallsvariable X ein,



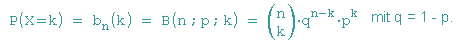
dann erhält man

E(X)=np

Bei Wikipedia findest Du hier die Umformung.

Setze in die allg. Formel für die Varianz



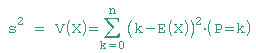
die Formel für E(X) ein sowie die Formel für die binomialverteilte Zufallsvariable X und zeige, dass gilt:



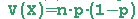
Die Eigenschaften für Binomialverteilungen findest Du in Mathebüchern und auch im Internet - oder aber Du variierst n und p im folgenden Applet und findest sie selber heraus: