- Zufallsgröße
- Erwartungswert
- Binomialkoeffizient
- Wahrscheinlichkeitsverteilung
- Verteilungsfunktion
- Wahrscheinlichkeitsfunktion
POISSON-Verteilung
Hat man eine lange Bernouilli-Kette (großes n) und gleichzeitig eine geringe Erfolgswahrscheinlichkeit p mit einem Erwartungswert, der gegen einen endlichen Wert strebt, dann ist die Berechnung des Binomialkoeffizienten, den man ja für die Binomialverteilung benötigt, lästig, da er sehr schnell mit n wächst.
Sinnvollerweise wird die Binomialverteilung dann durch eine Verteilung approximiert, die man für p gegen Null und n gegen unendlich erhält.
Simeon D. Poisson (1781 - 1840) stellte im Jahr 1837 für große n und kleine p eine gute Annäherung vor.
Ein gängiges Beispiel hierfür ist der radioaktive Zerfall. Aus einer sehr großen Anzahl von Atomen zerfallen pro Zeiteinheit nur sehr wenige. Der Zerfall ist zufällig und unabhängig von den bereits zerfallenen Atomen, der Erwartungswert ist endlich. Somit sind die Voraussetzungen für eine Approximation vorhanden.
Wir starten mit der Wahrscheinlichkeitsverteilung der Binomialfunktion:
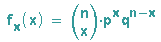
Für die Binomialverteilung gilt außerdem

und mit q=1-p und den Potenzgesetzen gilt auch:
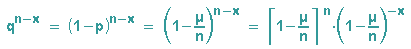
Wir setzen die beiden letzen Formeln sowie die Definition des Binomialkoeffizienten in fx(x) ein und erhalten:
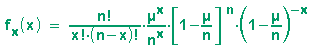
Diese Formel wird etwas umgestellt, der Binomialkoeffizient wird gekürzt:
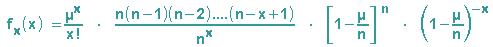
Sehen wir uns für n gegen unendlich die einzelnen Bestandteile an:
Teil 1: Die eckige Klammer: Um mit Tabellenkalkulation arbeiten zu können, nehmen wir mal an, der Erwartungswert sei 2.
Die folgende Abbildung verdeutlicht dann, dass die eckige Klammer für größer werdendes n gegen  strebt.
strebt.
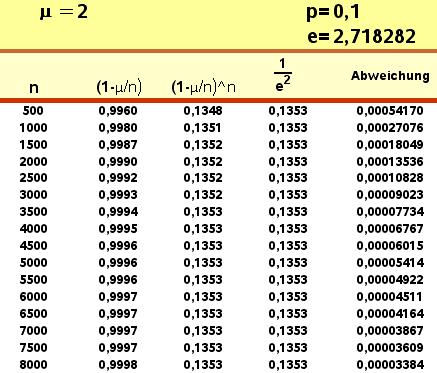
Teil 2: Die runde Klammer: Man sieht's mit bloßem Auge: Der Bruch wird Null, der Term in der Klammer strebt gegen 1, so bleibt's dann auch beim Potenzieren.
Teil 3: Der Bruch vor der eckigen Klammer: Man sieht's wieder mit bloßem Auge: Zähler und Nenner enthalten gleichviel Faktoren, für n gegen unendlich kann man kürzen, da dann die Subtrahenden vernachlässigbar klein sind und der Limes wird zu 1.
Mehr geht nicht und wir erhalten die POISSONVERTEILUNG:
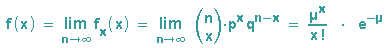
Im Internet könnt Ihr hier ein Applet der Projektgruppe "Neue Statistik", Hagen, sehen.
Schon bei relativ kleinem n wird die Binomialverteilung durch die Poissonverteilung recht gut angenähert:
|
|
Beispiele für die Annäherung der beiden Verteilungen schon bei kleinem n liefert "Kreyszig/Statistische Methoden und ihre Anwendungen, Vandenhoeck&Ruprecht, 1977" im entsprechenden Kapitel. Weitere dort beschriebene Anwendungen der Poissonverteilung: Tote durch Hufschlag in 10 preußischen Kavallerieregimentern in 20 Jahren, Zählung von Alphateilchen, Verkehrszählung in Graz 1963.
Erwartungsert und Varianz der Poissonverteilung
Der Erwartungswert der Poissonverteilung ist, wie aus der Herleitung ersichtlich

Allgemein gilt für die Varianz
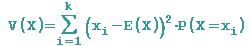
| © 2010-2024 Asti | PoVRay-Site |