The Platonic solids and Alan St. George

Alan St. George, British, retired architect, lives in Portugal and makes mathematical sculptures, including fractal variations on the regular (Platonic) solids.



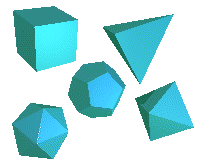
Euklid proved that there are exactly 5 solids that are bounded by regular polygons in such a way that the same number of side faces meet in the same way at each corner.

Tetrahedron, cube, octahedron, dodecahedron and icosahedron(4-flat, 6-flat, 8-flat, 12-flat and 20-flat)


Alan St. George sticks smaller solids of the same type onto these solids in a certain arrangement to create another Platonic solid. An example of how an octahedron is created from a cube:



Who doesn't know Rubic's Cube? In the style of this toy, the original cube is first divided into 27 smaller cubes. If you now take six small cubes whose edge length corresponds to that of one of the sub-cubes and make a cross out of them, on which another small cube is placed, you can place this structure on one of the 6 sides of ‘Rubic's Cube’ and you will then have an approximation of an octahedron. In the illustration, the cubes are shown slightly smaller for clarity. The resulting solid is bounded by a series of small squares. The cross with the attached cube is now placed on each of these square faces, whereby the new edge length is now 1/9 of the original edge length. Craft enthusiasts now have a hard time: they have to glue 36 medium-sized cubes onto our original cube, creating 6 x 21 free square faces, plus 6 x 4 free squares on our original cube: who has the patience to make 150 small cubes? Even if you stop at the 36 half-size cubes, you will realise that you can fractalise a cube into an octahedron in this way.



With his sculptures, Alan St. George has realised the transition from cube, tetrahedron and octahedron to any other of these three solids. (If you want to know how it's done, have a look in ‘Spektrum der Wissenschaft’, 10/97 - if you have collected them at home.Link ins Internet zu dieser Ausgabe.)

• Top of the page

In Euclid's (Greek mathematician, ca. 365 BC to ca. 300 BC) main work ‘Elements’, a 13-volume treatise on mathematics (plane geometry, figures, properties of numbers, ...), the so-called ‘Euclidean geometry’ is formulated, which formed the basis of geometry in general until the 19th century. The first translation from Arabic into Latin appeared in Venice in 1482. Euclid, who presumably learnt from Plato's students, taught geometry in Alexandria and also founded a school of mathematics there. He is also credited with various discoveries in the field of number theory.

• Top of the page