Animierte Isoflächen
Bekannt sind Isolinien:
Isobaren: Punkte gleichen Luftdrucks werden miteinander verbunden.
Isothermen: Punkte gleicher Temperatur werden miteinander verbunden.
Isohypsen: Punkte gleicher Höhe über dem Meeresspiegel werden miteinander verbunden (Höhenlinien).
Ebenso kann man bei 3-dimensionalen Flächen Raumpunkte mit gleichen Merkmalen miteinander verbinden und erhält dann Isoflächen.
Auf dieser Seite beschränke ich mich auf algebraische Flächen mit Singularitäten, die reelle Lösungen haben.
Im Internet gibt es sehr viele Darstellungen mathematischer Flächen (siehe Linksammlung), daher sollen hier nur einige Animationen vorgestellt werden.
Softwarelinks und Quellenangaben findet Ihr bei "Algebraische Flächen".
Betrachtet man die Gleichung x3 + y 2 - z 2 = 0, so besteht ihre Lösungsmenge aus allen Zahlentripeln (x/y/z), die beim Einsetzen in die Gleichung den Wert 0 ergeben. Stellt man diese Menge 3-dimensional dar, dann ist dies eine Isofläche.
Ebenso kann man jedoch auch die Gleichung x3 + y 2 - z 2 = a betrachten, ihre Lösungsmenge besteht dann aus den Zahlentripeln (x/y/z), die beim Einsetzen in die Gleichung den Wert a ergeben: Man erhält eine andere Isofläche.
Die ff. Animationen wurden mit PoVRay programmiert, bei Mausklick auf das Bild ist das Skript einsehbar.
Animationen können erzeugt werden durch Variation des Wertes von a oder anderer Parameter, aber auch durch eine "Kamerafahrt".
Zunächst werden die Flächen animiert, die im Programm SURFER vorgestellt werden: (Der Doppelkegel, das 1. Surferbeispiel, befindet bei der Begriffserklärung "Singularitäten")
Animationen 1, 2 und 3:
Kamerafahrt um den Koordinatenursprung für das Polynom x3 + y 2 - z 2 = 0.
Kamerafahrt um den Koordinatenursprung für das Polynom x3 + y 2 - z 2 = 1.
Kamerafahrt um den Koordinatenursprung für das Polynom x3 + y 2 - z 2 = -1.
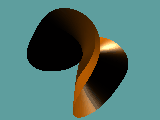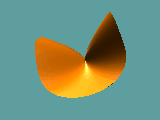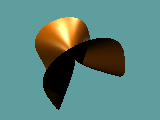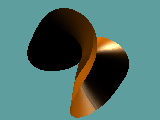 |
 |
 |
Animation 4:
Polynom x3 + y 2 - z 2 = a, mit a variierend von -1 bis +1.

Animation 6:
Polynom (x-b-a2)*(x-b+a2)*(x+b-a2)*(x+b+a2)+y2-z2 = 0
mit a=0,7 und b variierend von 0 bis +1.

Animationen 7, 8 und 9:
Kamerafahrt um den Koordinatenursprung für das Polynom
(x-b-a2)*(x-b+a2)*(x+b-a2)*(x+b+a2)+y2-z2 = 0
mit a=0,7 und b=0.
Kamerafahrt um den Koordinatenursprung für das Polynom
(x-b-a2)*(x-b+a2)*(x+b-a2)*(x+b+a2)+y2-z2 = 0
mit a=0,7 und b=0,3.
Kamerafahrt um den Koordinatenursprung für das Polynom
(x-b-a2)*(x-b+a2)*(x+b-a2)*(x+b+a2)+y2-z2 = 0
mit a=0,7 und b=0,6.
 |
 |
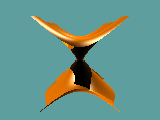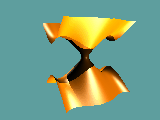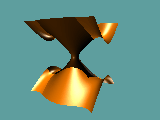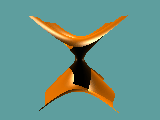 |
Animation 10:
Nochmal dasselbe Polynom mit =0,7 und b=1 in einen größeren "Container" gepackt, um 180° um die x-Achse und um 90° um die z-Achse gedreht.

In der Linksammlung links im Menü findet Ihr viele sehenswerte Seiten mit mathematischen Flächen.
| © 2009 Asti | Links für Unterricht | PoVRay-Site |
