- Einbettung in HTML-Dokumente
- Textausgabe
- Arbeiten mit Variablen
- Abfragen
- Zählschleifen
- Funktionen
- Objekte
- Operatoren
- Seitengestaltung
- Minirechner
- Links zu Javascript im Internet
- Startseite PoV-Kurs 1
- Startseite PoV-Kurs 2
- Startseite THEORIE
- Startseite
Zählschleifen
Zählschleifen dienen zum mehrmaligen Durchlauf eines Programmteiles.
Schleifen mit Anfangsbedingung
werden solange wiederholt, wie die Anfangsbedingung gültig ist: die Anzahl der Schleifendurchläufe steht von Anfang
an fest.
Beispiel: Ein beliebiger Text wird ausgegeben, solange eine Zählvariable kleiner als 3 ist,
die für die Schleife gütigen Anweisung müsen in geschweifte Klammern gesetzt werden:
Das zugehöige Skript:
<SCRIPT LANGUAGE="JavaScript">
<!--
for (zaehler=1; zaehler<=3; zaehler=zaehler+1)
//zaehler++ setzt den zaehler auch eins höher!
{
zahl =6
document.write("Das Quadrat von ",zahl, " ist ")
zahl=zahl*zahl
document.write(zahl ,"<br>")
}
// -->
</SCRIPT>
Auch rückwärts zählen ist möglich: (z.B. von 5 an, solange der Zähler größer als 3 ist)
Das zugehörige Skript:
<SCRIPT LANGUAGE="JavaScript">
<!--
for (zaehler=5; zaehler>3;zaehler--)
{
zahl =6
document.write("Das Quadrat von ",zahl, " ist ")
zahl=zahl*zahl
document.write(zahl ,"<br>")
}
//-->
</SCRIPT>
while-Schleifen: solange die Eintrittsbedingung erfüllt ist, werden Anweisungen immer wieder abgearbeitet. Da repeat-until-Schleifen nicht existieren, müssen sie mit negierter Abbruchbedingung als while-Schleife formuliert werden!
repeat { ............. } until ((a<=5) &&(b<=10))
wird ersetzt durch
while (! ( (a<=5) && (b<=10))) { ......... }
oder - unter Beachtung der de Morgan'schen Regel - (d.h. Vertauschung von AND und OR bei Verneinung von zusammengesetzten Aussagen)
while ((a>5) || (b>10)) {.............}
ist identisch zu:
Skript A:
<SCRIPT LANGUAGE="JavaScript">
<!--
a=8;b=13
while (! ( (a<=5) && (b<=10)))
{document.write("a = ",a, " und b = ",b, "<BR>");a=a-1; b=b-1 }
// -->
</SCRIPT>
Skript B:
<SCRIPT LANGUAGE="JavaScript">
<!--
a=8;b=13
while ( (a>5) || (b>10) )
{document.write ("a = ",a, " und b = ",b, "<BR>" );a=a-1; b=b-1
}
// -->
</SCRIPT>
Die de Morgan'schen Regeln
werden nicht nur in der Mengenlehre sondern auch in der Aussagenlogik benutzt:
Eine durch UND (AND) zusammengesetzte Aussage soll verneint werden. Sehen wir uns zunächst anhand eines Beispieles die Wahrheitstafel für UND an:
Aussage A: Ich gehe heute schwimmen.
Aussage B: Ich gehe heute spazieren.
Durch UND zusammgesetzte Aussage: Ich gehe heute schwimmen und spazieren.
Die Wahrheit sage ich nur, wenn ich BEIDES tue, also ist nur in Zeile 1 w(ahr), ansonsten f(alsch) für die durch UND zusammengesetzte Aussage einzutragen:
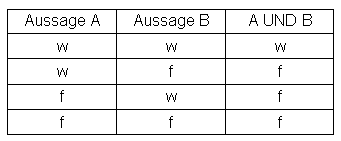
Eine durch UND zusammengesetzte Aussage ist also nur wahr, wenn beide Teilaussagen wahr sind.
Wie wird nun die durch UND zusammengesetzte Aussage verneint? Sehen wir auf unser Beispiel:
Es ist nicht wahr, dass ich heute schwimmen und spazieren gehe. Man kann mich einer Lüge überführen, sobald ich EINE der beiden Tätigkeiten nicht durchführe. Also gilt:
Ich gehe heute nicht schwimmen ODER ich gehe gehe heute nicht spazieren (oder tue Beides nicht) (inclusiv-ODER) ist gleichbedeutend mit Es ist nicht wahr, dass ich heute schwimmen und spazieren gehe. Für die Wahrheitstafel gilt also:
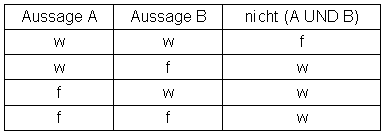
Eine durch UND zusammengesetzte Aussage wird verneint, indem beide Teilaussagen verneint und durch ODER verbunden werden.
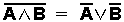
Der Überstrich steht für Verneinung, das "Dach" für UND, das v für ODER (lat.: vel vel) .
Bemerkung: Beim exclusiv-ODER wird über das v noch ein Punkt gesetzt.
Diese de Morgan'sche Regel kann nun auch in die Schaltalgebra übernommen werden.
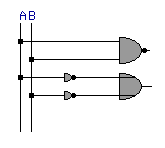
Anstelle eines NAND-Gatters kann auch ein ODER-Gatter, auf dessen Eingängen NICHT A und NICHT B liegen, geschaltet werden.
Der Negation einer Aussage entspricht in der Mengenlehre die Komplementmenge (Komplementärmenge) einer Menge:
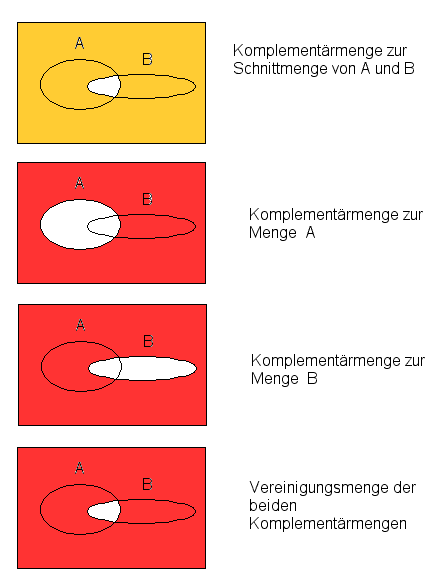
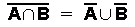
Die 2. de Morgan'sche Regel
Aussagenlogik: Vertauschung von UND und ODER
Schaltalgebra: Vertauschung von AND- und OR-Gatter
Mengenlehre: Vertauschung von VEREINIGUNG und SCHNITT.
Es gilt also:
Eine durch ODER verknüpfte Aussage wird negiert, indem die beiden Teilaussagen negiert und dann durch UND zusanmengesetzt werden .
Eine NOR-Schaltung kann ersetzt werden, indem die beiden Eingänge einer AND-Schaltung invertiert werden.
Das Komplement der Vereinigungsmenge zweier Mengen entspricht der Schnittmenge der beiden Komplementmengen.
| © 2010 Asti | PoVRay-Site | Mathematische Streiflichter |