Astis PoVRay - Seite, Kurs in Povray Klasse 8 bis 11, tutorial, Unterricht, education Unterrichtsmaterial Informatik Informatiunterricht

Alphakanalbilder

Erstellt man eine neue Grafik, so besteht das Bild zunächst aus einer Hintergrundebene, vorstellbar als Leinwand unter einem Gemälde. Sollen nur einzelne Bildbereiche verändert werden, so kann man eine neue Ebene öffnen, dort arbeiten, Bildelemente ändern ohne die erste(n) Ebene(n) zu beinflussen. Sollen nun Teile einer Ebene nicht sichtbar sein., so wird ein Graustufenbild, eine sog. Maske auf die Ebene gelegt, deren Grauwert bestimmt, wieviel von der maskierten Ebene sichtbar bleibt.

Um eine Maske zu erstellen, kopiert man den zu projektierenden Bildbereich mit Hilfe des "Zauberstabwerkzeugs" auf ein Bild mit transparenten Hintergrund.
Man wählt nun die Option "neue Maske erstellen" und speichert diese Maske in den Alphakanal des Bildes, sichert dann das ganze Bild in einem für PoVRay geeigneten Bildformat, z.B. im TGA-Format.

Der Alpha-Kanal ist ein Graustufenkanal, der für die Maskensicherung benutzt werden kann. Ein Kanal enthält alle Pixelinformationen für eine bestimmte Farbe: ein Kanal für Grausufenbilder, drei für Rot-Grün-Blau-Bilder.
Wird dieses Bild nun in PoVRay auf z.B. eine Kugel projiziert, dann ist der Bildhintergrund transparent, die Kugel wird nur dann sichtbar, wenn man ihr reflektierende oder lichtbrechende Eigenschaften zuteilt.
Die Deckfähigkeit der Ebene kann vor der Maskenerstellung verändert werden, man erhält dann eine graue Maske, die eine schwach durchscheinende Bildvorlage erzeugt: siehe rechte Spalte im Demobild oben!

Hier nochmals das Beispiel eines Skindapsus-Blattes: rechts der zugehörige Alphakanal

Das Bild kann nun für die Bildprojektion auf eine Kugel benutzt werden (vgl. Skript).

In der 1. Abbildung sieht man die Kugel sowie deren Schatten auf der Hintergrundebene.
In der 2. Abbildung wurde das Schlüsselwort "finish" weggelassen, "no_shadow" wurde ergänzt.
In der 3. Abbildung wurde "bump_map" weggelassen: das Blatt hat eine weniger erkennbare Struktur.

Anmerkung zu "BUMP_MAP":
Während bei image_map die Farben eines Bildes auf ein Objekt projiziert werden, beeinflusst bump_map den Normalenvektor zur Bildoberfläche, abhängig von der Bildfarbe: es scheint so, als ob das Bild auf die Oberfläche aufgeprägt sei. Sieh' dir die jeweiligen PoV-Skripte (per Mausklick) an!

Bevor es an die Aufgaben geht, hier wieder einige "Spickzettel":

Aufgaben:

Kopiere oder zeichne oder scanne oder fotografiere dir zwei geeignete Bilder, wähle in den Bildern geeignete Objekte aus, kopiere diese Bildteile in neue Bilder mit transparentem Hintergrund, speichere die Ergebnisse als al_v_01.tga und al_v_02.tga

Programmiere nun zwei Alpha-Kanal-Bilder, nenne sie alpha_01 und alpha_02

Zum Seitenanfang

Drehbankobjekte - lathe

Durch Angabe der x- und y-Koordinaten werden Punkte in der x-y-Ebene festgelegt, sodass dann bei Rotation um die y-Achse ein Drehobjekt entsteht. Die z-Komponente des zugehörigen Vektors wird als Null vorausgesetzt. Im Unterschied zum SOR (surface of revolution) unterscheidet das Drehbank-Objekt zwischen linearer, quadratischer und kubischer Verbindungslinie zwischen den angegebenen Punkten.

Während bei SOR dieselbe y-Koordinate nicht zweimal verwendet werden darf, ist dies beim Drehbank-Objekt erlaubt, die Bildumwandlungszeit ist dafür länger als bei SOR.

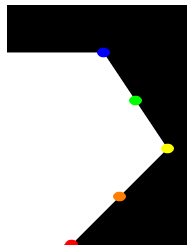
#declare Red_Point    = <1.00, 0.00, 0>
#declare Orange_Point = <1.75, 1.00, 0>
#declare Yellow_Point = <2.50, 2.00, 0>
#declare Green_Point  = <2.00, 3.00, 0>
#declare Blue_Point   = <1.50, 4.00, 0>

entsteht bei Verwendung linearer Verbindungslinien die ff. Form:

Ändert man nun die Punkte zu

#declare Red_Point    = <1.00, 0.00, 0>
#declare Orange_Point = <2.00, 1.00, 0>
#declare Yellow_Point = <3.50, 2.00, 0>
#declare Green_Point  = <2.00, 3.00, 0>
#declare Blue_Point   = <1.50, 4.00, 0>

und verwendet quadratische Verbindungslinien, so erhält man

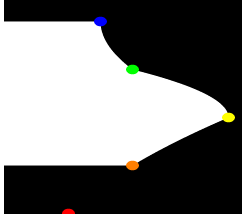Zwar sind die Punkte durch quadratischen Linienverlauf verbunden, der rote Punkt ist jedoch im Drehkörper nicht mehr enthalten: da man zur Definition einer Geraden nur zwei Bestimmungspunkte braucht, zur Definition einer quadratischen Funktion jedoch drei, verwendet POVRAY den ersten Punkt zur Bestimmung der Funktionsgleichung! Analog werden für kubische Funktionen vier Punkte benötigt.

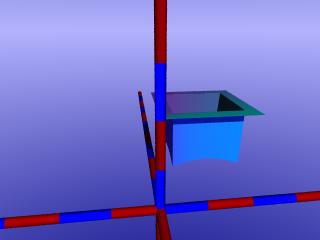
Mit dem Drehbank-Objekt kann man auf einfache Weise Tiegelchen und Töpfchen in allen Variationen produzieren. Per Mausklick ist das Skript des ff. Beispiels einsehbar.

Aufgaben

Programmiere unter Verwendung von lathe einen Trinkbecher, dessen Innenseite eine andere Farbe als die Aussenseite hat: (Dateiname: lathe_01.pov)

Verwende für den oberen Abschluss und den Henkel torus:

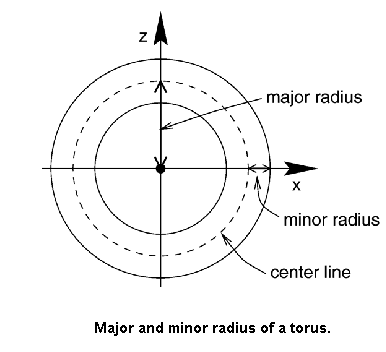
Programmiere unter Verwendung von lathe eine Vase oder eine Teekanne, oder eine Milchflasche (mit Inhalt) oder einen Kochtopf oder einen Kreisel ... o.ä. (Dateiname lathe_02.pov)
- Zum Seitenanfang
Polynome

Polynome sind Ausdrücke der Form a₀ +a₁x +a₂x² +a₃x³ + ... + a_nxⁿ. Dabei wird n der Grad des Polynoms genannt, die Zahlen a_i werden als Koeffizienten bezeichnet.

So ergibt bei graphischer Darstellung in der x-y-Ebene
y = f(x) = (x - 1)² - 3 = x² - 2x - 2
beispielsweise die um eine Längeneinheit nach rechts und um drei Längeneinheiten nach unten verschobene Normalparabel f(x) = x².

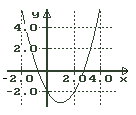
Im dreidimensionalen Raum ergibt x² + y² + z² - 1 = 0 eine Kugel mit Radius 1 LE,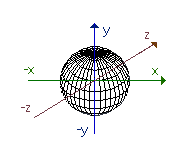

x² + y² - 1 = 0
ergibt einen unendlich langen Zylinder entlang der z-Achse mit Radius 1 LE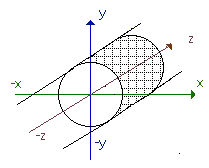

(bei Darstellung in der x-y-Ebene erhält man einen Kreis mit Radius 1 LE).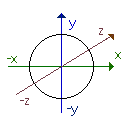

In PovRay werden Polynome 2.ten Grades durch das Schlüsselwort quadric definiert:
```
quadric { <A,B,C>, <D,E,F>, <G,H,I>, J }
```
wobei A bis J die ff. Koeffizienten sind:
```
  A x²    + B y²    + C z² +
  D xy    + E xz    + F yz +
  G x     + H y     + I z    + J = 0
```
Dabei ist zu beachten, daß die Reihenfolge der einzelnen Summanden anders als bei der Verwendung von poly ist !!!

Analog werden cubic (Polynom 3.Grades) und quartic (Polynom 4.ten Grades) verwendet.

Neben quadric, cubic und quartic können auch Polynome höherer Ordnung
(bx+cy+dz+e) ⁿ für n von 2 bis 7 definiert werden (lt. PovRay-Hilfe). Offensichttlich funktioniert die Verwendung von poly jedoch auch für n > 7, wie das Bild mit dem Stern zeigt.

Für die Syntax gilt:
```
poly {Grad des Polynoms, <a₀, a₁, . . . a_k>}
```
Die Anzahl m = k+1 der Koeffizienten wird durch
m = (n + 1) • (n + 2) • (n + 3) / 6
bestimmt, die a_i sind die Koeffizienten der einzelnen Summanden. Beim Bildumwandeln kann das Schlüsselwort sturm verwendet werden, um die Genauigkeit zu erhöhen.

Mit dem Programm DERIVE (mit dessen Hilfe die gängigen Aufgaben des Mathematikunterrichts u.a. gelöst werden können) kann man sich
(bx + cy +dz +e) ⁵
ausmultiplizieren lassen.

Beispiel eines Polynoms 5.ten Grades: a₀ x⁵+
a₁ x⁴ y + a₂ x⁴ z + a₃ x⁴ +
a₄ x³ y² + a₅ x³ y z + a₆ x³ y + a₇ x³ z² + a₈ x³ z + a₉ x³ +
a₁₀ x² y³ + a₁₁ x² y² z + a₁₂ x² y² + a₁₃ x² y z² + a₁₄ x² y z + a₁₅ x² y + a₁₆x² z³ + a₁₇ x² z² + a₁₈ x² z + a₁₉ x² +
a₂₀ x y⁴ + a₂₁ x y³ z + a₂₂ x y³ + a₂₃ x y² z² + a₂₄ x y² z + a₂₅ x y² + a₂₆ x y z³ + a₂₇ x y z² + a₂₈ x y z + a₂₉ x y + a₃₀ x z⁴ + a₃₁ x z³ + a₃₂ x z² + a₃₃ x z + a₃₄ x +
a₃₅ y⁵ + a₃₆ y⁴ z + a₃₇ y⁴ + a₃₈ y³ z² + a₃₉ y³ z + a₄₀ y³ + a₄₁ y² z³ + a₄₂ y² z² + a₄₃ y² z + a₄₄ y² + a₄₅ y z⁴ + a₄₆ y z³ + a₄₇ y z² + a₄₈ y z + a₄₉ y + a₅₀ z⁵ + a₅₁ z⁴ + a₅₂ z³ + a₅₃ z² + a₅₄ z + a₅₅ = 0

Aus der PovRay-Hilfe (DOS od. WINDOWS) geht nicht eindeutig die Reihenfolge der einzelnen Terme hervor. Jedenfalls wird nach absteigenden Potenzen von x geordnet (Summand Nr. 0 : x⁵, Summanden 1 bis 3: x⁴, Summanden 4 bis 9: x³, Summanden 10 bis 23: x², ... innerhalb dieser jeweiligen Gruppen wird dann nach absteigenden Potenzen von y und z geordnet). Die Reihenfolge scheint mit der von DERIVE übereinzustimmen.

In der Include-Datei shapesq.inc sind einige vordefinierte Polynome. Von den POVRAY-Autoren wird

    The CRC Handbook of Mathematical Curves and Surfaces
     David von Seggern
     CRC Press
     1990

empfohlen. Polynome können zusammen mit CSG verwendet werden, auch clipped_by ist erlaubt. Dabei wird das Innere eines Polynoms als Menge aller Punkte definiert, deren Koordinaten beim Einsetzen in die Polynomgleichung einen Wert kleiner als Null ergeben; ergeben ihre Koordinaten beim Einsetzten den Wert Null, so spricht man von der Oberfläche, für Werte größer als Null vom Äußeren.

quadric, cubic und quartic können mit poly definiert werden, Ebenen können als Polynome ersten Grades angesehen werden:
```
plane{<a,b,c>,d}
```
entspricht der Gleichung
```
 x  +  b y  +  c z  =  d
```
wobei nach dieser Definition der Normalenvektor, d.h. derjenige Vektor, der senkrecht zur Ebene steht, immer auf das "Äußere" der Ebene weist.

In der mathematischen Galerie von Tore Nordstrand werden viele schöne Beispiele von dreidimensionalen Flächen gezeigt, auch die zugehörigen Gleichungen und PovRay-Skripte werden zur Verfügung gestellt. Der Stern im ff. Bild ist aus einem von Tores Skripten entnommen:

Die beiden ff. Bilder sind Beispiele für Polynome 4.ten Grades (quartic).

Auch schon mit Polynomen 3.Grades kann man hübsche Effekte erzielen.

Nachfolgend nochmal zwei Beispiele für Polynome 5-ten Grades.

Aufgaben:
1. Programmiere ein Bild mit quadric: Dateiname pol_01
2. Programmiere ein Bild mit cubic: Dateiname pol_02
3. Programmiere ein Bild mit quartic: Dateiname pol_03
4. Programmiere ein Bild mit poly: Dateiname pol_04
- Zum Seitenanfang
Textobjekte

Das Textobjekt gehört zu den einfachen Objekten, die für CSG (Constructive Solid Geometry) benutzt werden können. Es kann verschoben, skaliert und rotiert werden. Eigenschaften wie Textur, Farbe, ... können wie üblich zugeordnet werden.

Im Windows-Font-Verzeichnis kannst du mit Hilfe des Dateimanangers nachschauen, welche Schriftarten auf dem PC, an dem du arbeitest, installiert sind. Notiere dir auf einem Zettel einige Fontnamen mit der Endung "ttf" (True Type Font).

Für die Syntax des Textobjektes gilt:
```
text {
    ttf "c:\windows\fonts\tahomabd.ttf" "PovRay" 1.9, <0.3,0.1,16>
    scale <...>
    rotate <...>
    translate <...>

    texture{...}
    finish {...}
  }
```
1. Der Verzeichnispfad für die Schriftart muss selbstverständlich dem eigenen PC angepasst werden.
2. Die Zahl nach der in Gänsefüßchen eingeschlossenen Zeichenkette steht für die "Tiefe" der Buchstaben,
3. der nachfolgende Vektor steht für den OFFSET, d.h. die Verschiebung der einzelnen Buchstaben in x-Achsen-, y-Achsen- und in z-Achsenrichtung.
Die beiden ff. Bilder kannst du wieder als "Spickzettel" benutzen.

Aufgaben:
1. Ein Bild mit Text: Dateiname "text_01.pov".
2. Ein Bild mit Text in einem Block aus beliebigem Material: Dateiname "text_02.pov".
- Zum Seitenanfang
Kameraeinstellungen

Aus der PoVRay-Hilfe hier die Abbildung für die vom Programm voreingestellte "Normalkamera":

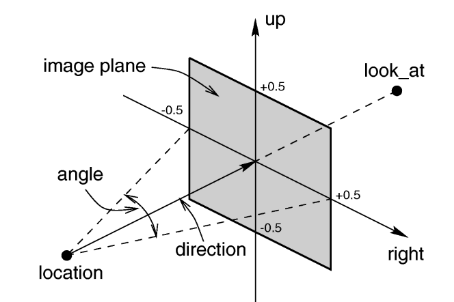
Mit Hilfe geeigneter Kameraeinstellungen kann das Bild wesentlich beeinflusst werden. Hier aus der PoV-Hilfe (Version 3.5) die Syntax für "camera":
```
CAMERA:
    camera{ [CAMERA_ITEMS...] }
CAMERA_ITEM:
    CAMERA_TYPE | CAMERA_VECTOR | CAMERA_MODIFIER |
    CAMERA_IDENTIFIER
CAMERA_TYPE:
    perspective | orthographic | fisheye | ultra_wide_angle |
    omnimax | panoramic | cylinder CylinderType | spherical
CAMERA_VECTOR:
    location  | right  | up  |
    direction  | sky 
CAMERA_MODIFIER:
    angle HORIZONTAL [VERTICAL] | look_at  |
    blur_samples Num_of_Samples | aperture Size |
    focal_point  | confidence Blur_Confidence |
    variance Blur_Variance | NORMAL | TRANSFORMATION
```
Fangen wir an mit dem KAMERA-TYP:

Folgende Möglichkeiten gibt es:
perspective | orthographic | fisheye | ultra_wide_angle | omnimax | panoramic | cylinder CylinderType | spherical (erst ab Version 3.5!)

Besser als viele Worte sind die ff. Beispiele:

Hier zunächst das Testbild: als voreingestellte Kamera wird perspective, d.h. die übliche Perspektive auf die Objekte benutzt. Das Schlüsselwort perspective darf hierbei weggelassen werden.

Bei orthografischer Sicht auf die Objekte wäre nur eine Kugel sichtbar, da die Kamera nun parallel verlaufende Lichtstrahlen benutzt. Der Bildausschnitt wurde daher für das ff. Skript in Höhe und Breite verachtfacht: die up- und right-Vektoren wurden mit 8 multipliziert.

Mit dem Schlüsselwort omnimax erhält man eine Kamera für Breitwandfilm:

Auch panoramic (Panorama = Rundblick, Ausblick) liefert ein ähnliches Ergebnis:

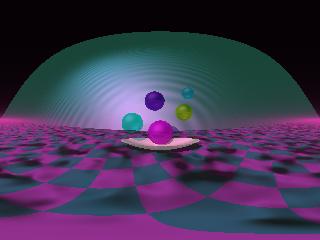
Mit fisheye wird das Bild auf eine Kugel projiziert:

Mit ultra_wide_angle wird das Bild auf ein Rechteck anstelle einer Kugel projiziert, dabei wird mit angle die Größe des Sichtwinkels festgelegt:

Bei der zylindrischen Projektion werden 4 Möglichkeiten unterschieden: (eine der Zahlen 1 bis 4 muss dem Schlüsselwort "cylinder" folgen.
vertikaler Zylinder, feste Blickrichtung
horizontaler Zylinder, feste Blickrichtung
vertikaler Zylinder, Blickrichtung bewegt sich entlang der Zylinderachse
horizontaler Zylinder, Blickrichtung bewegt sich entlang der Zylinderachse

Kamera-Abänderungen (modifier):
```
CAMERA_MODIFIER:
    angle HORIZONTAL [VERTICAL] | look_at |
    blur_samples Num_of_Samples | aperture Size |
    focal_point  | confidence Blur_Confidence |
    variance Blur_Variance | NORMAL | TRANSFORMATION
```
Auch bei einer Kamera kann das Schlüsselwort normal benutzt werden: die Lichtstrahlen werden dann entsprechend dem benutzten Muster abgelenkt: (im Beispiel die Muster spiral und bumps)

Mit dem Schlüsselwprt focal_point (Brennpunkt) zusammen mit aperture (Blendenöffnung: je größer die Blendenöffnung, desto kleiner der scharfe Bildausschnitt) und blur_samples, das die Anzahl der Lichtstrahlen, die auf einen Bildpunkt treffen, bestimmt, kann die Bildschärfe eingestellt werden:

Als letztes noch ein Beispiel zu einer eigenen Definition einer Kamera mit #declare oder #local:

Beispiel:

Mit
```
#declare lange_Brennweite=
  camera {
   location -z*100
   angle 3
  }
```
oder
```
#declare Short_Lens =
  camera {
   location -z*50
   angle 15
  }
```
kann eime eigene Kamera definiert werden.

Aufgaben:

Programmiere ein Bild deiner Wahl (Dateiname kam_00.pov) und teste dann 4 verschiedene Möglichkeiten für Kameraeinstellungen an diesem Bild (Dateinamen kam_01.pov bis kam_04.pov).
- Zum Seitenanfang
Felder (arrays)

In PovRay gibt es ein- oder mehrdimensionale Felder (arrays). Ein eindimensionales Feld kann man sich als eine Liste vorstellen, die Listenelemente sind dabei über Indizes ansprechbar und müssen vom gleichen Datentyp sein. Sie müssen definiert (initialisiert) werden.

Beispiel für ein eindimensionales Feld aus drei Elementen:
```
#declare Schöne_Texturen=array[3];
#declare Schöne_Texturen[0]=pigment {Jade}
#declare Schöne_Texturen[1]=pigment {Water}
#declare Schöne_Texturen[2]=pigment {Red_Marble}
```
Hierfür gibt es auch eine abkürzende Schreibeweise:
```
#declare Schöne_Texturen=array[3](Jade,Water, Red_Marble);
```
Eine Fehlermeldung ergäbe
```
#declare Schöne_Texturen[1]=normal {dents 0.5}
```
da hier nicht der gleiche Datentyp vorliegt. Eine Fehlermeldung würde auch die ff. Zeile ergeben:
```
 #declare Oberfläche=Schöne_Texturen[3]
```
da ein solches Listenelement oben nicht definiert (initialisiert) wurde.

Gut geeignet sind Felder z.b. für die Definition eigener Farben, Oberflächenstrukturen, Texturen, ...:

Mehrdimensionale Felder können mit bis zu 5 Dimensionen deklariert werden.
```
#declare MeinFeld = array[4][10]
```
Hiermit wird ein Feld aus 40 Elementen, das 4 Reihen und 10 Spalten hat, deklariert.
```
#declare Digits =
 array[4][10]
 {
  {7,6,7,0,2,1,6,5,5,0},
  {1,2,3,4,5,6,7,8,9,0},
  {0,9,8,7,6,5,4,3,2,1},
  {1,1,2,2,3,3,4,4,5,5}
 }
```
Zwischen den Elementen und den Dimensionen müssen Kommata gesetzt werden. Zum Aufruf der Elemente schreibt man Digits[0][0] bis Digits[4][10].

Im ff. Bild entspricht die y-Koordinate der Kugelposition der 4. Zeile eines mehrdimensionalen Feldes.

Im Folgenden soll ein Beispiel für die Verwendung eines mehrdimensionalen Feldes gezeigt werden:
8 Kugeln sollen in den Ecken eines Würfels der Kantenlänge 2 LE positioniert werden. Zunächst werden die unteren 4 Kugeln gesetzt:

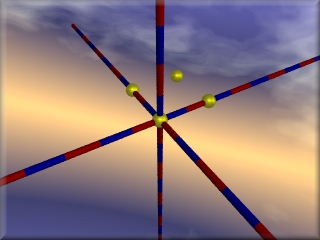
Dies kann mit
```
union{
        sphere {<0,0,0>, 0.25}
        sphere {<2,0,0>, 0.25}
        sphere {<2,0,2>, 0.25}
        sphere {<0,0,2<, 0.25}

          finish{F_MetalA}
          pigment {Yellow}
        }//end union
```
ereicht werden. Definiert man jedoch ein 3x4-Feld wie folgt:
```
#declare Pos = array[4][3]
                    {  {0,0,0},
                       {2,0,0},
                       {2,0,2},
                       {0,0,2}
                     }
```
dann kann man statt dessen auch wie folgt schreiben:
```
union{
        sphere {<Pos[0][0],Pos[0][1],Pos[0][2]>, 0.25}
        sphere {<Pos[1][0],Pos[1][1],Pos[1][2]>, 0.25}
        sphere {<Pos[2][0],Pos[2][1],Pos[2][2]>, 0.25}
        sphere {<Pos[3][0],Pos[3][1],Pos[3][2]>, 0.25}
          finish  {F_MetalA}
          pigment {Yellow}
        }//end union
```
Dies kann nun mit einer Zählschleife abgekürzt werden: schaut man sich den Aufruf der Feldelemente genau an, so sieht man, dass die Zeilennummer von 0 bis 3 läuft. Also schreibt man:
```
#local i=0;
#while (i<4)
    sphere {<Pos[i][0],Pos[i][1],Pos[i][2]>, 0.25
          finish{F_MetalA}
          pigment {Yellow}}
    #local i=i+1;
#end
```
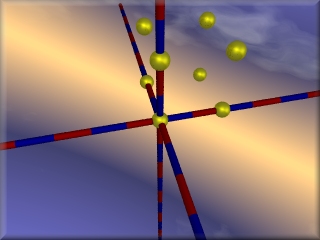
und erhält genau dasselbe Bild. Genau so kann man nun mit den 4 darüberliegenden Kugeln verfahren. Oder aber man schreibt die Programmzeile, die "sphere" enthält nochmal mit einem um 2 erhöhten y-Wert:
```
#local i=0;
#while (i<4)
  union{
    sphere {<Pos[i][0],Pos[i][1]  ,Pos[i][2]>, 0.25 }
    sphere {<Pos[i][0],Pos[i][1]+2,Pos[i][2]>, 0.25 }
          finish{F_MetalA}
          pigment {Yellow}
        } //end union
    #local i=i+1;
#end
```
Aufgaben:
1. Programmiere ein Bild deiner Wahl. Verwende dabei ein eindimensionales Feld mit mindestens 5 Farben, die einander ähnlich sind. Dateiname array_01.pov
2. Programmiere ein Bild deiner Wahl. Verwende dabei ein eindimensionales Feld mit mindestens 3 Elementen (Textur oder Oberflächenstruktur). Dateiname array_02.pov
3. Programmiere analog zum "Würfelbild" ein "Quaderbild" für einen Quader mit den Kantenlängen 2 LE, 3 LE und 4 LE. Dateiname array_03.pov
4. Programmiere unter Verwendung eines Feldes mindestens ein Bild, das auch schön anzuschauen ist. Dateiname array_04.pov
- Zum Seitenanfang
Isoflächen

Die Gleichung x² + y² - 4 = 0 stellt bekanntlich einen Kreis um den Koordinatenursprung mit Radius r = 2 dar. Analog kann 3-dimensional die Gleichung für eine Kugeloberfläche angegeben werden: x² + y² + z² - 4 = 0.

Betrachtet man die Relation R = x² + y² + z² - 4 und sucht sich all die Punkte heraus, für die R denselben Wert hat, so erhält man die Punkte, die auf der Oberfläche der Kugel liegen, falls R = 0: isosurface.

Mit dem Kennwort isosurface können nun Funktionen selbst definiert werden oder auf vordefinierte Funktionen zurückgegriffen werden. Die Dokumentation ist leider nicht allzu umfangreich.

Eine ISO-Oberfläche ist näherungsweise (der Grad der Annäherung entspricht dabei den Einstellungen) die Oberfläche einer 3-dimensionalen Funktion. Da solche Funktionen sich meist unendlich weit vom Koordinatenursprung ausbreiten, muss mit dem Schlüsselwort
contained_by {...}
eine räumliche Begrenzung vorgenommen werden.
```
isosurface {
  function { FUNCTION_ITEMS }
  [contained_by { SPHERE | BOX }]
  [threshold FLOAT_VALUE]
  [accuracy FLOAT_VALUE]
  [max_gradient FLOAT_VALUE]
  [evaluate P0, P1, P2]
  [open]
  [max_trace INTEGER] | [all_intersections]
  [OBJECT_MODIFIERS...]
}
```
Für die voreingestellten Werte gilt:
```
contained_by : box{-1,1}
threshold    : 0.0
accuracy     : 0.001
max_gradient : 1.1
```
So. hier erst mal wieder die "Spickzettel":

Aufgabe: Eine Abbildung mit ISO-Surface: Dateiname iso_01.pov
- Zum Seitenanfang
Höhenfelder

Höhenfelder (heightfields) sind Würfel der Kantenlänge 1 LE, deren obere Fläche gebirgig ist. Der Würfel liegt in der x-z-Ebene, seine vordere linke untere Ecke befindet sich im Koordinatenursprung. Die Höhe jedes Punktes hängt von der Palettenfarbe der verwendeten Grafikdatei ab. (Im Beispiel die Palette für ein Graustufenbild mit 256 Farben: die Nummerierung des Farbindex beginnt bei Farbe Nr. 0 und endet bei Farbe Nr. 255.)

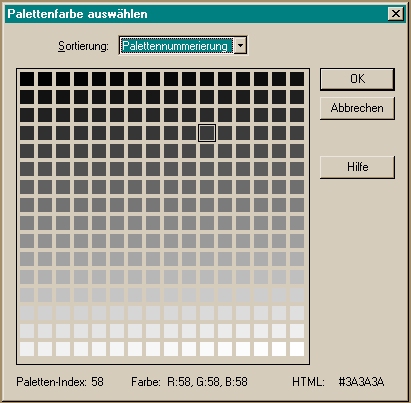
Dabei spielt die Auflösung des verwendeten Bildes für die Skalierung des Höhenfeldes keine Rolle. Bei höherer Auflösung wird das Höhenfeld weicher gezeichnet.

Die zughörige PoVRay-Syntax ist: (wobei die selben Bildformate wie bei "image_map" erlaubt sind.)
```
height_field { gif "bildname.gif" pigment {... }}
```
Die linke Bildvorlage im TGA-Format ergibt das Bild rechts:

Werden Bilder mit schwarzem Hintergrund (Palettenindex 0) gewählt, so liegt der "Würfelboden" des Höhenfeldes genau in der x-z-Ebene.

Bei Invertierung der Bildvorlage scheint das Höhenfeld gespiegelt zu sein:

Mit der folgenden od. ähnlichen Vorlagen kann eine Landschaft realisiert werden:

Dazu kann dann noch das Schlüsselwort "water_level" benutzt werden: Der Parameter ´water_level´ gefolgt von einer Zahl zwischen 0 und 1 kann nach dem Bildnamen hinzugefügt werden, sodaß unterhalb dieses Wertes das Höhenfeld nicht angezeigt wird. (Beispiel: ´water_level 0.5´ heißt, daß nur die obere Hälfte des Höhenfeldes grafisch umgesetzt wird. Auf diese Weise können unerwünschte tiefere Werte weggeschnitten werden. Das Schlüsselwort ´smooth´ glättet das Höhenfeld.

Aufgaben:
1. hoeh_01: Programmiere ein Höhenfeld derart, dass zwei geometrische Figuren (Kreis, Quadrat, Raute, Rechteck, Stern, Pfeil, ...) gut sichtbar sind und verschiedene Höhen haben. Nenne die Vorlagengrafik hvor_01.tga (oder ~.gif)
2. hoeh_02: Programmiere deinen Vornamen als Höhenfeld. Nenne die Vorlagengrafik hvor_02.tga (oder ~.gif)
3. hoeh_03 und hoeh_04:
4. hoeh_05 und hoeh_06:
Auch mit einem Passfoto von dir kannst du arbeiten: das Bild muss in Graustufen umgewandelt werden, es sollte mehrmals stark weichgezeichnet werden, damit die Konturen nicht zu hart werden. Beim zweiten Beispiel wurde eine Glaskugel um das Höhenfeld gelegt. In beiden Beispielen wurde mit Hilfe von "union" noch eine geeignete Box an das Höhenfeld gelegt.
- Zum Seitenanfang