Die Programmiersprache persistance of vision raytracer

Ein Bild wird aus einem Textskript berechnet, indem der Weg von Lichtstrahlen simuliert wird. Die Benutzer/innen geben die Position einer Kamera, einer oder mehrerer Lichtquellen und Objekte an. Eigenschaften von Kamera, Lichtquellen und Objekten sind im Skript festlegbar. Wird dabei eine bestimmte Syntax beachtet, dann wird das Textskript von PoVRAy in eine fotorealistische Computergrafik umgerechnet. Die Syntax dieser Programmiersprache ist identisch zu der von C++ und Java, und wird hier spielerisch erlernt.

Ein PoVRAy-Skript beteht im wesentlichen aus 3 Teilen:

1. Der Programmkopf: Hier stehen die Kommentare (Autor/in), Datum, Programmname, ...
   Hier werden auch die sog. INCLUDE-Dateien eingebunden. Dies sind (analog zu den UNITS in PASCAL) Dateien, in denen Objekte, Farben, Makros, ... festgelegt werden können
2. Der Deklarationsteil: Hier werden (globale) Variable definiert, d. h. solche, die für das ganze Programm gültig sein sollen, wie z. B. #declare Blau_01=color rgb <0.57, 0, 0.834> ;
   Deklarationen werden mit einem Semikolon abgeschlossen.
3. Der Verarbeitungsteil: Hier werden die Objekte angegeben, deren Eigenschaften, was mit ihnen geschehen soll.

Ein einfaches Beispiel:



Das Programm ist Freeware und kann somit kostenfrei auf euren privaten Rechnern installiert werden.

• Zum Seitenanfang

Geometrische Körper

... sind in PoVRay vordefiniert. Weitere Definitionen finden sich in den Dateien Shapes.inc, Shapes2.inc und Shapesq.inc. Auch eigene Körper können definiert werden.

Die Kugel

sphere{  <3, 3, 0>,  3
    pigment {color Blue}
    finish {F_MetalA}
    normal{bumps 0.5}
}//Ende der Kugel

sphere{  <xm, ym, zm>,  radius
    pigment {color Blue}
    finish {F_MetalA}
    normal{bumps 0.5}
}//Ende der Kugel

xm, ym und zm geben den Kugelmittelpunkt an.

finish (Oberflächenbeschaffenheit: Reflexionseigenschaften, Umgebungslichtstärke, Streulichtstärke, Lichtreflexgröße, Brechungseigenschaften bei Gläsern, ... ) und

normal (Oberflächenstruktur: Beulen, Wellen, Zähne, ... ) dürfen weggelassen werden, pigment (Farbe) kann durch

texture (Material: Holz, Glas, Marmor, Stein, ... ) mit einem dazugehörigen Schlüsselwort ersetzt werden. In der Datei textures.inc sind Materialien vordefiniert.

Beispiele für finish:

 finish {
   ambient 0.5
   diffuse 0.35
   reflection 0.2
        }//Ende Finish

finish {F_MetalA}

finish {Glass_Finish}

Beispiele für pigment:

 pigment {color Red}

 pigment {color red 0.372549 green 0.623529 blue 0.623529}

 pigment {checker color Red color Yellow scale 3 rotate <0,20,0>}

 pigment {Red_Marble scale <3,10,1>}

 pigment {Blue_Sky3}

In der Datei colors.inc findest du weitere Schlüsselwörter für Farben, in textures.inc für Materialien, Farben und Oberflächenbeschaffenheiten.

Die ff. Bilder zeigen Kugel, Kegel, Zylinder, Quader und Ebene. Per Mausklick auf das Bild ist jeweils das zugehörige Skript einsehbar:







Die Ebene wird durch die folgenden Syntax bestimmt:

plane {y, -4
  pigment {color ...}
  finish{...}
  }//Ende der Ebene

Im Beispiel steht die Ebene senkrecht auf der y-Achse und liegt eine Einheit unter dem Koordinatenursprung.

• Zum Seitenanfang

Das Koordinatensystem

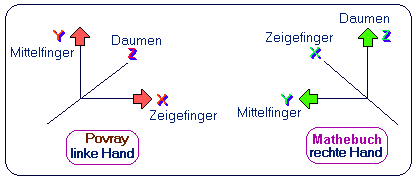PovRay hat ein linkshändiges Koordinatensystem: die x-Achse und die y-Achse liegen in der "Monitorebene": x weist nach rechts, y weist nach oben. Die z-Achse steht senkrecht zur Monitorebene und weist in den Monitor hinein, daher wird häufig die Kameraposition in der -z-Richtung gewählt, was den Blickwinkel der Benutzer/innen vor dem Bildschirm ergibt.

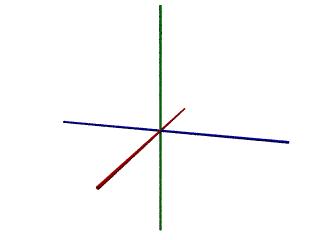
Aufgabe K1:
Erstelle eine Datei koord.POV, die ein Koordinatensystem darstellt, die 3 Achsen sollen verschiedene Farben haben, sie sollen von x = - 10 bis x = +10, y = -10 bis y = +10 und z = -10 bis z = +10 reichen. Achte auf sinnvolle Position von Kamera und Lichtquelle, wähle für die Bildumwandlung Anti-Aliasing = 0.3.


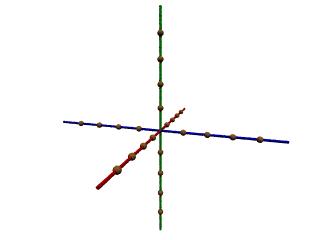
Aufgabe K2:
Erstelle eine Datei koord2.POV, die als Markierung bei den Längeneinheiten 2,4,6,8, -2, -4, -6 und -8 kleine Kugeln in Kontrastfarbe zu den Achsen positioniert. Versehe deine Skript-Datei mit geeigneten Kommentaren. Tippe nicht alles neu, sondern benutze "kopieren/einfügen" !



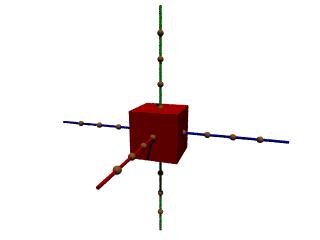
Aufgabe K3:
Speichere nun Koord2.pov als Koord3.pov und füge eine Box ein, die von der Ecke <-2,-2,-2> bis zur Ecke <2,2,2> reicht.



Aufgabe K4:
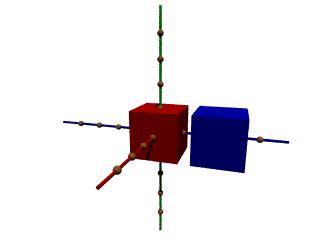
Speichere nun Koord3.pov als Koord4.pov und füge eine 2. andersfarbige Box ein, die mit translate <5,0,0> um 5 Einheiten in Richtung der x-Achse verschoben wurde.

An dieser 2. Box soll nun eine Drehung getestet werden: Mit rotate <0,dreh,0> wird diese Box nun um den Winkel "dreh" um die y-Achse gedreht.



Aufgabe K5:
Probiere verschiedene Winkel aus, z.B. Schritte von 30°. Sichere eine dieser Dateien unter dem Namen Koord5.



Was stellst du fest bei Eingabe eines "positiven" Winkels, bei Eingabe eines "negativen" Winkel?

Aufgabe K6:
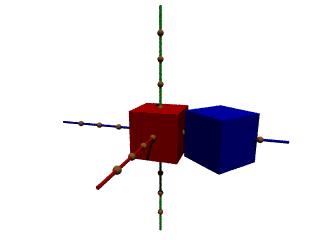
Speichere nun Koord5.pov als Koord6.pov und vertausche die beiden Zeilen für Verschiebung und Drehung. Was stellst du fest?



Aufgabe K7:
Speichere nun Koord6.pov als Koord7.pov.
Die dritte Abbildung ist die Vergrößerung: scale <1,2,1> vergrößert (im Beispiel: verdoppelt) in Richtung der y-Achse, scale 2 verdoppelt in allen 3 Richtungen.

Stelle nun ein Bild her (aus dem du zum Schluss das Koordinatensystem entfernst), das auch etwas schöner aussieht.

Benutze verschiedene Körper, die gedreht, verschoben und skaliert werden.

Benutze verschieden Texturen, Farben, Oberflächenstrukturen für die einzelnen Körper, füge auch eine Hintergrundebene ein.

Beispiele zur Anregung aber ohne Skript:

• Zum Seitenanfang

Constructive Solid Geometry (CSG) - Teil 1

Mit union, difference und intersection können Körper zusammengesetzt werden:



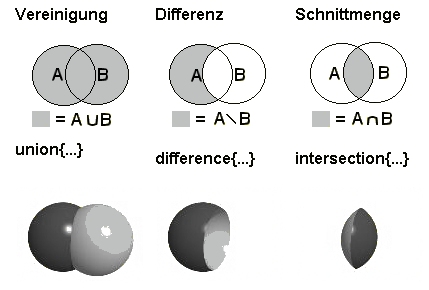Beide Anweisungen werden zum Verbinden von verschiedenen Objekten zu neuen Objekten benutzt, Solche Objekte kann man gemeinsam einfärben und/oder zusammen abbilden (mittels scale, rotate, translate). So kann man z. B. ein Mensch-Ärgere-Dich-nicht-Männchen oder eine Schachfigur aus verschiedenen Grundkörpern zusammensetzen.

Der öffnende Schnitt mit clipped_by{...}:
Der Effekt ist ähnlich dem bei der Schnittmengen-Bildung und bei der Differenzmenge. Übrig bleibt, was in beiden Körpern enthalten ist. Im Vergleich zur Schnittmengenbildung mit intersection ist der Körper jedoch dort geöffnet, wo er von der Oberfläche des Körpers in den Klammern von clipped_by{...} geschnitten wird.

Aufgabe csg_01:
Fertige mit union eine Raupe aus Kugeln. Kopiere, verschiebe und skaliere dann diese Raupe, so dass zwei davon in einem Bild erscheinen. Ändere bei der 2. Raupe die Texturen oder die Farben.



Aufgabe csg_02:
Fertige eine Lupe als Schnittmenge zweier Kugeln. Bemerkung: Zwei geeignete Kreise auf Kästchenpapier helfen vielleicht eurem Vorstellungsvermögen ein bisschen weiter!

Mit interior {ior 1.75} kann ein Brechungsindex von Glas simuliert werden. Probiere verschiedene Werte im Bereich von 0,2 bis 2,0 aus!



Aufgabe csg_03:
Fertige eine Mauer mit rechteckigem Durchgang (hier soll später ein Fenster eingebaut werden. Eine mögliche Textur ist:

texture{
    pigment{
       brick Gray40, color Scarlet
       brick_size <6,3,6>*.35
       mortar 1/8
        }
     normal {bumps .8 scale 0.1}

Aufgabe csg_04:
Baue nun mit deiner Mauer ein Zimmer mit 3 Wänden, die jeweils ein Fenster haben. Die Kamera soll in dieses Zimmer hineinzeigen. Benutze rotate und translate. Wenn du mit den Größen nicht mehr zurechtkommst, dann kopiere dein Koordinatensystem in dieses Textskript dazu. Achte auf die Reihenfolge von rotate und translate!

Die anschließende Bilderfolge zeigt dir einen langsamen Aufbau des Zimmers.




Aufgabe csg_05:
Na ja, was ist ein Zimmer ohne Decke. Wenn ihr nicht im Regen stehen wollt, dann muss eine Zimmerdecke her!




Aufgabe csg_06:
Dein Textskript mit der Szenenbeschreibung ist jetzt (trotz der Kommentare, die du hoffentlich eingefügt hast !!!) etwas lang und dadurch unübersichtlich geworden. Darum werden wir unser Zimmer nun in eine INCLUDE-Datei verlagern.

1. Markiere alles, was zum Gemäuer gehört mit der Maus und kopiere es in den Windows-Zwischenspeicher mit STRG-C.
2. Öffne eine neue PoVRay-Datei (leer) und füge den Text mit STRG-V ein.
3. Speichere diese neue Datei schon mal unter dem Name ZIMMER.INC
4. Ergänze sie nun wie folgt:

   #declare zimmer=object {
        union {
   
         ... hier steht der eingefügte Text ...
   
              }//end union
        }//end object
   

   Speichere nochmals als ZIMMER.INC
5. Nimm nun csg_05.pov und füge oben bei den Standard-Include Dateien ein: #include zimmer.inc
6. Lösche alle Zeilen, die für die Zimmerkonstruktion waren. (Vorher eine Sicherheitskopie anfertigen!!!
7. Füge ein: object {Zimmer}
   Das Ergebnis müsste genau das selbe sein!!!

Bemerkung: Immer, wenn du eigene umfangreiche Szenenbeschreibungen hast, kannst du sie in INCLUDE-Dateien auslagern. Du kannst dir auch eine eigene Farbdatei farben.inc schreiben, in der du Farben über


#declare Blau_01 = rgb <0.57, 0.0, 0.62  >;

selbst definiertst.

Aufgabe csg_07:
So - wer will schon, dass der Wind durch alle Fenster bläst: Also nimm Millimeterpapier, Bleistift und Geodreieck und beginne mit der Fensterdefinition. Fertige eine ähnliche größere Zeichnung und füge noch ein Fensterkreuz in der Mitte dazu. Überlege dir dann, welche Koordinaten die jeweiligen Quader haben, sodass du die Ecker der Boxen bestimmen kannst.

Beispiel:
Für den linken Balken gilt:

box {<0,0,0> <dicke,hoehe, tiefe> texture {Material}}

Die Größen dicke, hoehe, tiefe werden vorher mit

#declare dicke=1;
#declare hoehe=12;

usw. festgelegt.

Noch ein zweites Beispiel für das innere Fensterkreuz:

//senkrechte Innenstange
box {<breite/2-dicke_kreuz/2,dicke>
     <breite/2+dicke_kreuz/2,hoehe-dicke,tiefe>
     texture {Material_kreuz}}

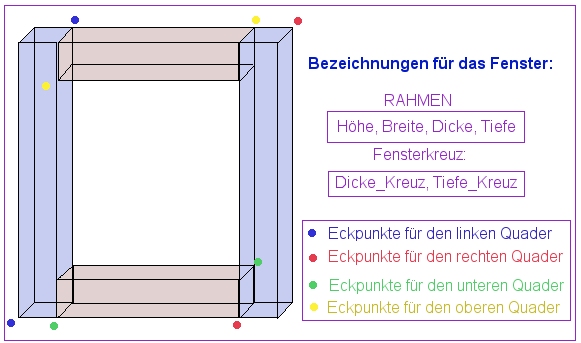Wenn der Rahmen fertig ist, dann werden Glasscheiben eingesetzt. Das Ergebnis wird dann in eine Datei Fenster.inc geschrieben.



Aufgabe csg_08:
Die Datei fenster.inc wird in das "Zimmerskript" eingebunden, das Fenster dann über object {Fenster rotate ... translate ... scale ... } in die passenden Stellen der Zimmerwände eingefügt.

Und jetzt wäre es Zeit, auch etwas schöner anzuschauende Bilder zu programmieren!

• Zum Seitenanfang

Constructive Solid Geometry (CSG) - Teil 2

Die folgenden Konstruktionsbeschreibungen und ein Teil der Bilder stammen mit freundlicher Genehmigung von Friedrich Lohmüller.

Aufgabe csg2_01
Programmiere ein Mensch-Ärgere-Dich-Nicht-Männchen. Verwende dabei die ff. Konstruktionsbeschreibung, die dessen Ansicht von vorn in die +z-Richtung zeigt.



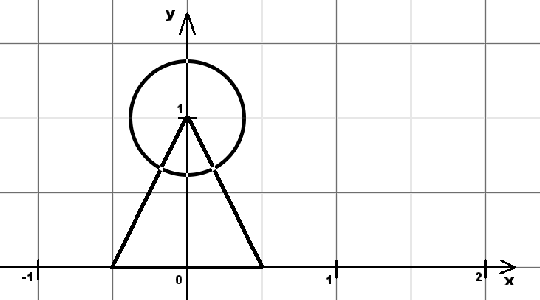Aufgabe csg2_02
Programmiere einen Würfel aus Rohren m.H. der ff. Konstruktionsbeschreibung, die die Ansicht aus allen drei Richtungen zeigt.





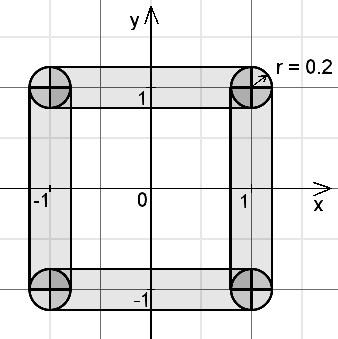Aufgabe csg2_03
Als nächstes ist ein Bogen für eine Brücke an der Reihe. Benutze wieder die vorliegende Konstruktionsbeschreibung: Sie zeigt die Ansicht von vorn und von rechts.



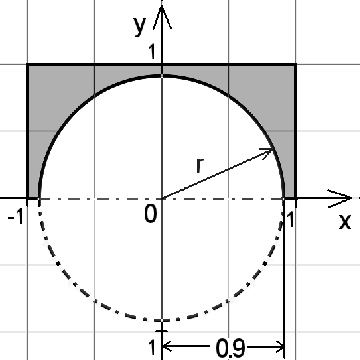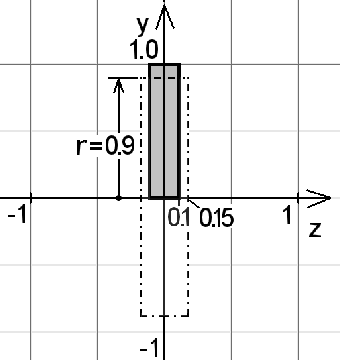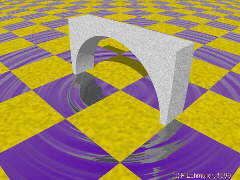Aufgabe csg2_04
Ein bisschen komplizierter wird es noch: Hier ist unser Ziel:



... und hier auch die Konstruktionszeichnung



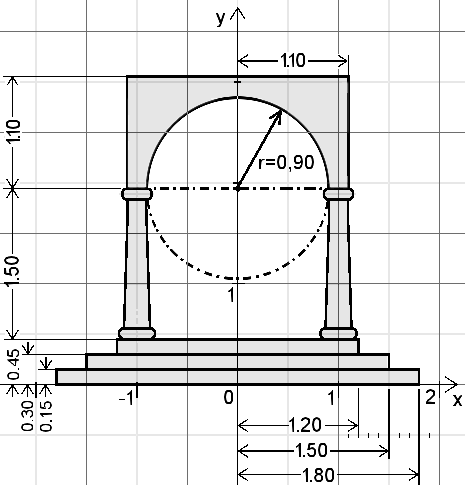Aufgabe csg2_05
... ist freiwillig: Ein Türmchen mit Fenstern soll programmiert werden. Sieh dir die Konstruktionsbeschreibung an:



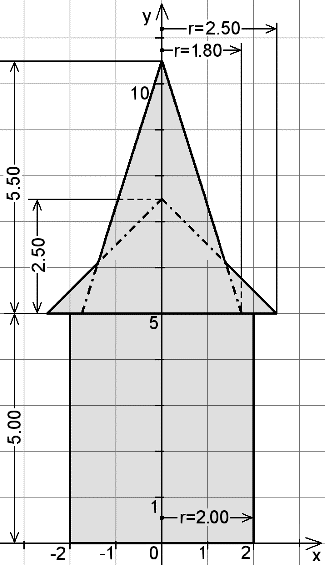Aufgabe csg2_06
... ist natürlich auch freiwillig: Wer will schon in einem fensterlosen Turm seine Zeit verbringen:
Zunächst wird der Turmkörper ausgehöhlt. Sodann werden die Löcher für die Fenster abgezogen um anschließend an denselben Stellen die vordefinierten Fenster einzusetzten.





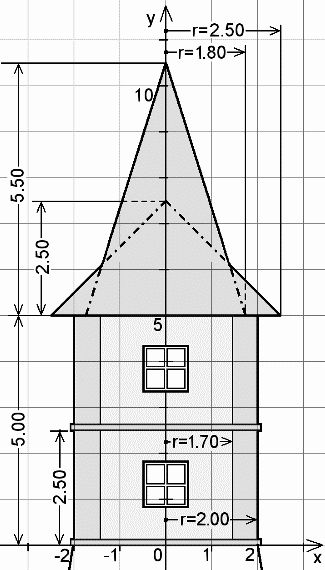Na und wenn du das alles geschafft hast, dann bist du einfach Spitze und nichts mehr hindert dich daran, Friedrich Lohmüllers Schlösschen nachzubauen oder aber ein ähnliches Gemäuer auf die Beine zu stellen:



Du hast immer noch nicht genug? Dann kommt hier der letzte Vorschlag für die echten Fans und Könner/innen:



... und das Lohmüller'sche Logo wirst du natürlich durch dein eigenes Logo ersetzen! Viel Erfolg und viel spaß!

• Zum Seitenanfang

Arbeiten mit Makros

1. Bei manchen Programmieraufgaben kommt es vor, dass relativ komplizierte Programmteile mehrmals wiederholt werden müssen. Sollen z.B. in einer Szene um einen Tisch herum 4 gleichartige Stühle hingestellt werden, dann würde die vierfache Definition des Stuhles diese Szenenbeschreibung stark vergrößern.
   
2. Ein Problem wurde in einer anderen Aufgabe bereits gelöst: es wäre gut, darauf zurückgreifen zu können.
3. Ein Objekt wird in einer Szenenbeschreibung mehrmals benötigt, jedoch mit anderer Größe, Material, Farbe, ...

Mit MAKROS (ähnlich wie Prozeduren in der Programmiersprache PASCAL) wird ein solches Detailproblem so allgemein gelöst, dass es immer wieder verwendbar ist.

Beispiel: Jemand möchte eine Bildergalerie programmieren: Ein rechteckiger Rahmen wird mehrmals benötigt. Höhe, Breite, Dicke, Tiefe und Material sind jedoch jeweils verschieden.

Mit

#macro Tisch (variable_1, variable_2, variable_3, ...)
 ..... Anweisungen ..........
#end

wird das Makro definiert. Mit seinem Namen wird es dann aufgerufen.
Falls gewünscht ist, dass es verschoben, skaliert, rotiert, ... werden soll, ist es sinnvoll, es in eine "union" oder in "object" einzubinden. Am folgenden Beispiel erkennst du am besten, wie es funktioniert:

Lösung:

1. Schritt: Im Deklarationsteil werden breite, hoehe, ... festgelegt.
   Mit difference {...} wird der Rahmen programmiert.
   Mit union {...} wird eine Verschiebung um die halbe Breite und Höhe nach links bzw. unten vorgenommen, so dass die Rahmenmitte sich im Koordinatenursprung befindet.
   
   
   
   
   
   
2. Schritt: In union wird noch eine "Papierscheibe" (=box) eingefügt, auf die später das gewünschte Bild projiziert wird.
   Die Farbe wird zunächst auf White gesetzt, dies wird später durch image_map ersetzt und variabel gewählt.
   
   
   
   
   
   
3. Schritt: Durch #macro Bilderrahmen (breite, hoehe, dicke, tiefe, rahmen_material)... #end wird das Makro definiert.
4. Schritt: Durch
   

   Bilderrahmen (3, 6, .2, 0.13,
      texture{Red_Marble
         scale 0.35
         finish {F_MetalA}
          }//end texture
                    )//end Bilderrahmen

   
   wird es aufgerufen.
   
   Die Deklarationen für breite, hoehe, ... können jetzt im Pov-Skript gelöscht werden, da die notwendigen Parameter beim Aufruf des Makros festgelegt werden.
   Da die Texturen-Definition im Makro-Aufruf unübersichtlich ist, kannst du die Textur vor dem Aufruf mit declare festlegen: #declare meine_texture = texture {.....}
   
   
   
   
   
   
5. Schritt: Um das Makro auch skalieren, verschieben und rotieren zu können, ist es sinnvoll, es in ein Objekt zu packen:
   
   

   object{
     Bilderrahmen (8,6,.57,0.8,mein_material_1,mein_bild_1)
       scale 0.65
       translate <-3,0.5,0>
   }//end object
   

   
   Die Definitionen von mein_material_1, mein_bild_1, mein_material_2 und mein_bild_2 stehen nun im Deklarationsteil des Programmes.
   
   
   
   

Aufgaben Mak_01, Mak_02, Mak_03, Mak_04:
4 Bilder mit Makros programmiert, kommentierte und übersichtliche Listings im Heft, ebenso die Ausdrucke der 4 Bilder im Kleinformat auf einer einzigen DIN A4 Seite.

Themenvorschläge: Bilderrahmen mit Zylindern programmiert, Seifenblasen, Baukastenklötzchen, Mobiles mit verschiedenen Objekten, einfach zu realisierende Einrichtungsgegenstände, Teegläser und Trinkbecher, Leuchttürme, Kirchtürme, Häuser, Triangeln, Boote, Lampen, Brillen, Bleistifte, Buntstifte, Mensch-Ärgere-Dich-Nicht-Klötzchen, Töpfe, Kannen, Leitern, Regale, Autoreifen, Leiterwagen, Spielzeuglokomotiven, Spielzeugeisenbahnen, Spielzeugautos, .... und alles, was dir selber einfällt! Es müssen nicht unbedingt gegenständliche Bilder sein.

• Zum Seitenanfang

Zählschleifen

Auch hier geht es um Elemente, die sich wiederholen. Mit der WHILE - Schleife stellt PoVRay eine Wiederholungsanweisung zur Verfügung:
Betrachte die folgenden Zeilen und überlege dir, welches Bild entsteht!!!

#declare zaehler=0;

#while (zaehler<11)
   sphere {<zaehler,0,0>}, 0.25
              pigment {color Red}
           }//end sphere
   #local zaehler=zaehler+1;
#end

Erkärung:
Zunächst wird die Variable zaehler auf 0 gesetzt, danach wird gefragt, ob zaehler kleiner als 11 ist. Da die Antwort noch "ja" lautet, wird eine Kugel mit dem Mittelpunkt <0,0,0> gezeichnet. Die Variable zaehler wird nun um 1 erhöht.
Der Compiler kehrt zurück zur Abfrage, ob der Zähler immer noch kleiner als 11 ist. Da die Antwort wieder "ja" lautet, wird nun eine Kugel mit dem Mittelpunkt <1,0,0> gezeichnet. usw..... Nach der Kugel mit dem Mittelpunkt <10,0,0> ist zaehler nicht länger kleiner als 11, die Schleife wird beendet.

Anstatt in den Kugelmittelpunkt kann der Zähler auch z.B. in "rotate" eingebaut werden.

Aufgaben zae_01 bis zae_06

Programmiere die folgenden Bilder:

1. Einen in der x-z-Ebene liegenden Kreis aus Kugeln


2. Einen in der x-y-Ebene liegenden Kreis aus Kugeln
3. Einen in der y-z-Ebene liegenden Kreis aus Kugeln
4. Ein in der x-z-Ebene liegendes Quadrat aus Kugeln


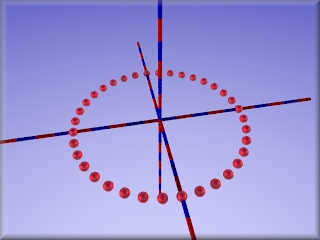Hierzu brauchst du zwei ineinandergeschachtelte Zählschleifen: Nimm zunächst Papier und Bleistift und erstelle eine Tabelle für i und j: wo werden die Kugeln jeweils gezeichnet?



union{
  #declare j=0;
  #while (j<11)

        #declare i=0;
        #while (i<11)
           sphere{  <0,0,-1>,  0.25
              pigment {Red}
              finish {F_MetalA}
              translate <i,0,j>

           }//end sphere
        #declare i=i+1;
        #end

  #declare j=j+1;
  #end
}//end union





5. Ein in der x-y-Ebene liegendes Quadrat aus Kugeln


6. Ein in der y-z-Ebene liegendes Quadrat aus Kugeln

Aufgabe zae_07:

Wenn du noch eine dritte Zaehlschleife um die beiden ersten herum baust, erhältst du einen Würfel:



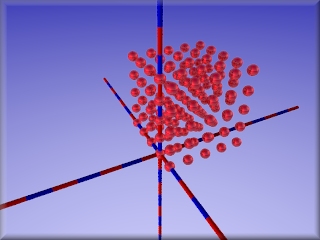Aufgabe zae_08:

Stelle einen "Kugelquader" mit den "Längen" a= 3, b=4 und c=5 "Kugeleinheiten" her.

Aufgabe zae_09:

Mache aus dem Kreis aus der ersten Zählschleifenaufgabe eine Spirale:



Aufgabe zae_10:
Ja, jetzt heißt es, vier Bilder mit Zählschleifen zu programmieren, die auch schön anzuschauen sind. Dateinamen: zae_10a bis zae_10d.

Einige Beipiele, um die Fantasie anzuregen: (und außerdem als "Spickzettel" verwendbar)



Auf freiwilliger Basis noch einige Übungen:

• Zum Seitenanfang

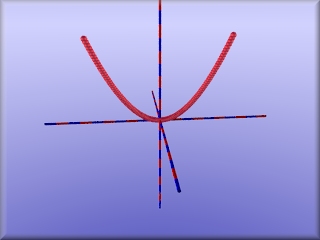Schnurbilder mit Zählschleifen

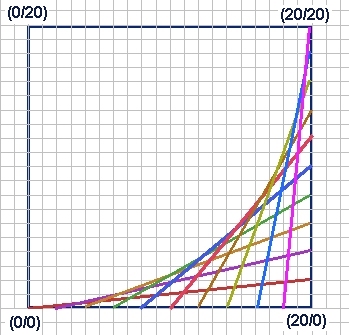In der Abbildung seien A₁ bis A₁₀ die Startpunkte (untere Seite) der Linien, B₁ bis B₁₀ seien die Endpunkte.

Aufgabe Schnur01

1. Schreibe die Koordinaten der Anfangs- und Endpunkte in eine Tabelle in dein Heft.
2. Schau dir die Koordinaten genau an. Welche Regelmäßigkeit stellst du fest?
3. Halte diese Regelmäßigkeit schriftlich fest:
   Für die Anfangspunkte gilt:
   Die x-Koordinate geht von ... bis ... in Schritten von ...
   Die y-Koordinate geht von ... bis ... in Schritten von ...
   
4. Schreibe dasselbe für die Endpunkte auf.
5. Die Linien sollen in PoVRay mit Zylindern dargestellt werden.
   
   

   cylinder {<0,0,0> <20,2,0> 0.25
      pigment {....}
      finish {....}
     } //end cylinder
   

   
   Überlege dir nun, wie du eine Zählschleife programmieren kannst, die Zylinder entsprechend der Abbildung darstellt.
   Führe dies in einem PoV-Skript durch. Speichere das Bild als schnur01.pov.

Aufgabe Schnur02
Programmiere einen passenden Rahmen aus Zylindern oder Quadern. Programmiere einen passenden Hintergrund, füge deine Zählschleife aus Aufgabe Schnur01 ein. Speichere unter Schnur02.pov.

Aufgabe Schnur03
Programmiere drei "Schnurbilder" und speichere sie als sch_03a, sch_03b und sch_03c.

Hier die Denkanstöße:

• Zum Seitenanfang

Funktionen

Auch Funktionen, die du aus dem Matheunterricht kennst, sind mit PoVRay über eine Zählschleife einfach darstellbar. Im 1. Beispiel die Sinus-Funktion von 0 bis 2*pi.



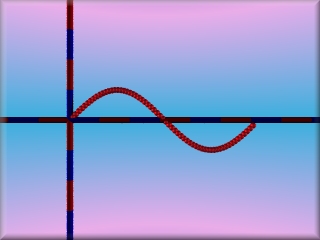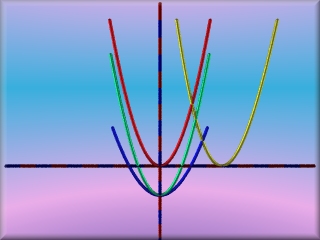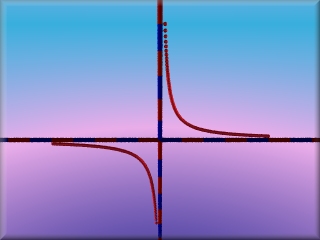Am 4. Beispiel siehst du, dass durch das Einfügen einer Rotation 3-dimensionale Bilder entstehen.

Aufgabe Funk_01
Stelle in einem Bild die Geraden y = -2x+4 und y = 0,5x-2 dar. Dazu soll ein x-y-Koordinatensystem gezeigt werden.

Aufgabe Funk_02
Stelle in einem Bild die Relation y = Wurzel(x) dar. Dazu soll ein x-y-Koordinatensystem gezeigt werden.

Aufgabe Funk_03
Baue zu einer Zählschleife mit einer Funktion deiner Wahl eine äußere Zählschleife zusätzlich ein, sodass ein Rotationskörper entsteht.

Aufgabe Funk_04
Mindestens ein Bild, das auch schön fürs Auge ist, muss her!

• Zum Seitenanfang

Fallunterscheidungen

SWITCH, CASE, RANGE, IF

PoVRay bietet mehrere Möglichkeiten zum bedingten Bildumwandeln. Nicht nur bei der Erstellung von Animationen, sondern auch beim Erzielen anderer Effekte ist dies nützlich.

Teil 1: Der Schalter SWITCH

... kann zusammen mit case (Mehrfachabfrage) oder range (Bereichsabfrage, d.h. von ... bis ...) benutzt werden.

Für die Syntax des Schalters switch in Verwendung mit case gilt:

#switch (Variable)
     #case (Variablenwert_1)
        ..........
     #break  //beendet Fall 1

     #case (Variablenwert_2)
        ..........
     #break  //beendet Fall 2

     #case (Variablenwert_3)
        ..........
     #break  //beendet Fall 3

     #else
        ..........   //alle übrigen Fälle

#end //beendet die Fallunterscheidung

Falls die Variable den Wert Variablenwert_1 hat, wird der erste Teil des Skripts umgewandelt, bei Variablenwert_2 der zweite Teil, usw. ...

Beispiel:

#switch (Farbwechsel)

   #case (1)
         pigment {color DarkOrchid}
   #break

   #case (0)
         pigment {color MediumAquamarine}
   #break

#end

Dabei ist Farbwechsel eine Variable, die innerhalb einer Zählschleife ihren Wert dauernd von 1 zu 0 und 0 zu 1 wechselt. Im Beispiel "fall_01.pov" wird dieses Beispiel verwendet.



Im nächsten Beispiel nimmt Farbe nacheinander die Werte 1, 2, 3, ... zaehler an. Für die Werte 1, 2 und 3 wird mit "case" eine Farbe festgelegt, in allen übrigen Fällen wird mit else die Farbe "white" festgelegt.


Teil 2: Abfragen mit #if ... #end

In einer Kugelreihe soll jede 10 Kugel rot gefärbt sein, alle übrigen sollen eine andere Farbe haben.

1. Information



2. Mit MODULO (in PoVRay als mod abgekürzt) kann der Rest bei einer ganzzahligen Division festgestellt werden:
3. Es gilt: 17 : 5 = 3 Rest 2
4. Es gilt also: 17 mod 5 = 2
5. Lässt man also einen Zähler die Werte 1 bis 100 annehmen und fragt, ob zaehler mod 10 = 0, so erhält man die Vielfachen von 10, wenn die Antwort "ja" ist.
   Denn: 10 mod 10 = 0, 20 mod 10 = 0, ....
6. Für die Syntax von mod gilt: mod (zahl1,zahl2)

Da hier nur zwei Möglichkeiten betrachtet werden (der Divisionsrest ist 0 oder von Null verschieden), wird die IF-Abfrage benutzt.



Teil 3: Noch eine Mehrfachabfrage mit #case ... #end unter Verwendung von MODULO.

Eine Kegelreihe soll aus 10 sich regelmäßig wiederholenden Farben bestehen. Wieder wird mit MODULO programmiert, diesmal jedoch - da hier eine Mehrfachabfrage vorliegt - benutzen wir case statt if.



Teil 4: Abfrage eines Bereiches mit range

Die Kegelreihe soll nun aus 4 Farben bestehen:

1. Zähler von 00 bis 09: 1. Farbe
2. Zähler von 10 bis 19: 2. Farbe
3. Zähler von 20 bis 29: 3. Farbe
4. Zähler von 30 bis 39: 4. Farbe (41. Kegel weglassen)

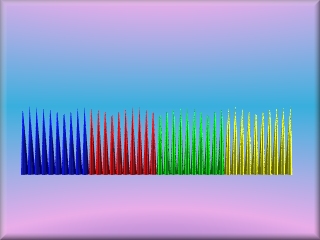Aufgabe Fall_01

Programmiere einen Kreis aus 100 Kügelchen, sodass jede 10. Kugel rot ist, die übrigen sollen weiß sein:




Aufgabe Fall_02

Programmiere einen Kreis aus 100 Kügelchen, sodass die ersten 25 Kugeln eine erste Farbe haben, die zweiten 25 Kugeln eine 2. Farbe haben, usw. ...




Aufgabe Fall_03

Programmiere einen Kreis aus 20 Kügelchen, sodass je 5 Kugeln sich regelmäßig wiederholende Farben haben.



Aufgabe Fall_04

Programmiere einen Kreis aus 40 Kügelchen, sodass zwei alternierende Farben vorhanden sind, benutze IF und MOD.



Aufgabe Fall_05

Zwei schöne Bilder fehlen noch! Dateinamen fall_05a und fall_05b.




Ein Hinweis zum ersten Bild: mit transmit 0.75 kannst du die Farbei zu 75% (im Beispiel) transparent machen.
Mit color rgb <0.3, 0.5, 0.7> kannst du eigene Farben definieren, die sich aus rot, grün und blau zusammensetzen.

• Zum Seitenanfang

Zufallszahlen

Pascalprogrammierer/innen kennen die Funktion RANDOM, die Zufallszahlen zwischen 0 und 1 (inklusive) erzeugt und mit dem Befehl RANDOMIZE initialisiert werden muss, damit nicht immer dieselbe Folge von Zahlen entsteht. Analog dazu bietet POVRAY die Funktionen rand, die aus einer Folge von Zufallszahlen von Null bis Eins eine ausgibt, und seed, mit der ein Startwert festgelegt wird, um gleiche Zahlenfolgen zu vermeiden.

Verwendbar sind rand und seed,, wenn z.B. eine Folge von Objekten zufällig verteilt werden oder aber eine Farbe zufällig variiert werden soll.




Ein Beispiel, das uns eine Anzahl zufällig verteilter Kugeln, deren Farbe ebenfalls zufällig ausgewählt wird, liefert, wird jetzt in Schritten besprochen:

1. Schritt: Erstelle ein neues Programm, speichere es als zuf_01.pov.



2. Schritt: Im Programmkopf stehen wie üblich die Kommentarzeilen, die gewünschten INCLUDE-Dateien werden jetzt eingebunden.



3. Schritt: Im Verarbeitungsteil werden Kamera und Lichtquellen sowie ein Koordinatensystem eingefügt, dazu noch eine "Himmelskugel" als Hintergrund.



4. Schritt: Mit
   
   

   #declare VERSCHIEBUNG = seed(17);
   #declare KUGELRADIUS = seed(15);
   

   
   werden im Deklarationsteil die Größen VERSCHIEBUNG für die Kugelmittelpunkte und KUGELRADIUS für die Radien initialisiert. Die Zahlen 17 und 15 sind beliebig.



5. Schritt: In den Verarbeitungsteil kommt nun unsere Zählschleife z.B. für 20 Kugeln: (Mausklick aufs Bild zeigt dir das Skript.)
   
   



6. Schritt: Warum wurde bei den Mittelpunktskoordinaten jeweils 0.5 subtrahiert, warum danach mit 10 multipliziert?



7. Schritt: Warum sind nur 18 Kugeln zu sehen? Was ändert sich, wenn du die Zahlen für die Initialisierung änderst? Sind danach mit Bestimmtheit alle 20 Kugeln zu sehen?
   
   



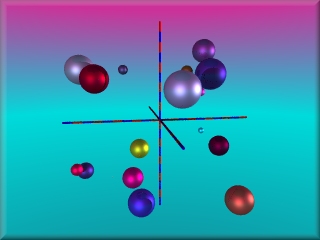
8. Schritt: Sinnvoll ist eine Abfrage, die bewirkt, dass nur diejenigen Kugeln gezeichnet werden, deren Abstand vom Koordinatenursprung eine bestimmte Entfernung nicht überschreitet.
   
   Dazu wird die Funktion vlength benutzt, die die Länge des Vektors vom Punkt <0,0,0> zum Kugelmittelpunkt <xm, ym, zm> berechnet:
   
   vlength(Mittelpunkt)
   
   



9. Schritt: Im Deklarationsteil werden drei neue Größen Abstand, Kugelzahl und Anzahl deklariert. Nur wenn die Länge des Mittelpunktvektors kleiner als Abstand ist, wird die Variable Kugelzahl um eins erhöht, sobald Kugelzahl
so groß wie Anzahl ist, wird der Schleifenzähler j auf seinen höchsten Wert gesetzt, und die Schleife wird beendet.

Hier also ist die komplette Zählschleife:



#local j=0;

#while (j<500)
   #local Mittelpunkt=<(rand(VERSCHIEBUNG)-.5)*10,
                          (rand(VERSCHIEBUNG)-.5)*10,
                          (rand(VERSCHIEBUNG)-.5)*10>*2;

   #if (vlength(Mittelpunkt)<Abstand)
        #sphere { Mittelpunkt, rand(KUGELRADIUS)*2
          pigment{color rgb< rand(VERSCHIEBUNG),
                                rand(VERSCHIEBUNG)-.2,
                                rand(VERSCHIEBUNG) >}
          finish{F_MetalA}}
         //end sphere

        #local kugelzahl=kugelzahl+1;
        #if (kugelzahl=Anzahl+1) #local j=499; #end

        #else

        #local j=j+1;
   #end //end if
   #local j=j+1;
#end //end while

Aufgaben zuf_01 bis zuf_05

Programmiere je ein Bild (beim 1. Beispiel kannst du spicken) mit zufällig verteilten Zylindern (01), Würfeln (02), Tori (03), Kegeln (04) und Blobs (05). Denke auch ans Ausdrucken der Skripte und Bilder. Bringe dein Heft in Ordnung!!!

• Zum Seitenanfang

Rekursionen

"Rekursion" stammt aus dem Lateinischen und bedeutet "Zurückführung". Ein Objekt ist dann rekursiv, wenn es Varianten von sich selbst enthält oder mit Hilfe von Varianten seiner selbst definiert ist (z.B. Geschichten innerhalb von Geschichten, Bilder innerhalb von Bildern, ...).



Teil A:

Eine einfache Art, ein Bild im Bild herzustellen, ist das mehrmalige Umwandeln des Bildes, das selbst als Vorlage dient:
Mit Hilfe des Schlüsselwortes image_map wird das Bild als Pigment auf ein Objekt projiziert. Nicht alle Bildformate sind dabei in PoVRay zugelassen: gif | tga | iff | ppm | pgm | png | sys | sind erlaubt, alle übrigen Formate erzeugen eine Fehlermeldung.

Trägt man in der Datei povray.ini die Zeilen

;TGA-Bildausgabe
Output_File_Type=T

ein, so erhält man das (verlustfrei komprimierte) und erlaubte TGA-Bildformat.

Für die Syntax von image_map gilt:

pigment{image_map {tga "bibi_02.tga" interpolate 2  map_type 0
               once //falls einmalige Projektion erwünscht
               }//end image_map
   scale 12
   rotate 45
   translate <.65,1.08,0>
   }

Bedeutung von map_type:

1. map_type 0: ebene Bildprojektion.
2. map_type 1: kugelförmige Bildprojektion: Stellt man sich eine Kugel im Koordinatenursprung vor, dann entspricht die y-Achse der Nord-Süd-Richtung, Ober- und Unterkante des Bildes berühren ohne auf eine Skalierung Rücksicht zu nehmen, die beiden Pole. Das Bild wird um die Kugel gewickelt.
3. map_type 2: zylindrische Bildprojektion.
4. map_type 5: Das Bild wird um einen Torus gewickelt.

Mit interpolate 2 oder interpolate 4 kann das Bild geglättet werden.

In den folgenden Beispielen kannst du wieder per Mausklick das Skript einsehen.





Aufgabe rek_01:
Programmiere drei "Bilder im Bild", nenne sie rek_01a, rek_01b und rek_01c.

Teil B:
Eine 2. Art, rekursiv zu programmieren ist die folgende: Man definiert sich ein beliebiges Objekt, dieses wird dann benutzt, um ein 2. Objekt zu definieren, mit Hilfe des 2. Objektes wird das 3. Objekt definiert .....
Mit Mausklick kannst du wieder das jeweilige Skript einsehen.

• Zum Seitenanfang

Vektorfunktionen

Funktionen kennst du aus dem Mathematikunterricht der 9. Klasse. Zuordnungen zwischen den Elementen zweier Mengen werden Relationen genannt. Eine Funktion liegt dann vor, wenn es zu jedem Element der Ausgangsmenge höchstens ein Element der Zielmenge gibt.

Vektoren kennst du aus dem Physikunterricht der 10. Klasse: es sind Größen, die eine Richtung und eine Länge haben. Parallel verlaufende Vektoren gleicher Länge werden dabei nicht voneinander unterschieden. Geometrisch werden Vektoren durch einen Pfeil dargestellt, zu ihrer Kennzeichnung werden kleine lateinische Buchstaben benutzt, über die ein kleiner Pfeil gesetzt wird.





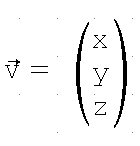
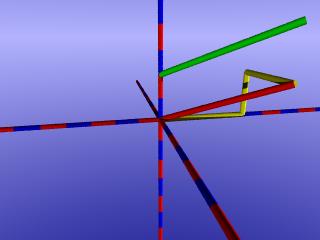Geht man vom Ursprung aus 4 LE in x-Richtung, 2 LE in y.Richtung und 3 LE in minus-z-Richtung (jeweils in gelber Farbe dargestellt), so erhält man den roten Vektor in obiger Abbildung.

Der um zwei Längeneinheiten nach oben verschobene (grüne) Vektor wird mathematisch ebenfalls durch

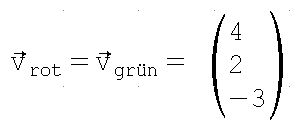
dargestellt.

Für die Abbildung mit PoVRay muss jeweils der Anfangs- und Endpunkt des jeweiligen Zylinders angegeben werden: Vergleiche das Skript zur Abbildung!


Zu PovRay gehören eingebaute Vektorfunktionen. Ihnen können ein oder mehrere Argumente übergeben werden, der Funktionswert (Rückgabewert) kann ein Vektor oder eine Zahl sein. Zwei dieser Funktionen sollen hier näher betrachtet werden. Eine dritte Vektorfunktion, nämlich VLENGTH, die die Länge eines Vektors bzw. den Abstand eines Punktes vom Koordinatenursprung berechnet, kennst du bereits.

a) vrotate(A,B)

Für eine Drehung um den Koordinatenursprung kann vrotate(A,B) benutzt werden: A ist dabei der Vektor vom Koordinatenursprung zu einem gegebenen Punkt P(x,y,z). B ist der Drehvektor, durch dessen Komponenten festgelegt wird, um welche Koordinatenachse und um welchen Winkel der gewünschte Punkt gedreht wird.
Im ff. Beispiel wird um die y-Achse um 40° gedreht. Mit Mausklick kannst du das Skript einsehen.

Im Deklarationsteil des Skriptes werden Startpunkt, Drehvektor und Kugelmittelpunkt vereinbart.

#declare Startpunkt1=<6,4,0>;
#declare Drehvektor=<0,10,0>;
#declare Mittelpunkt=vrotate(Startpunkt1,Drehvektor);

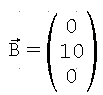als Drehvektor gibt an, dass um die y-Achse gedreht wird.

ist der Startpunkt P, der gedreht wird.

Der Drehwinkel 40° wird in der Zählschleife festgelegt:

#local Drehvektor=Drehvektor+ <0,40,0>;

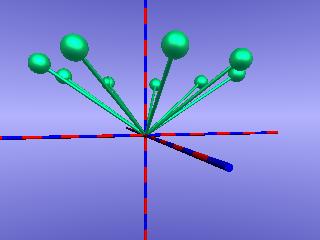Ersetzt man in der Zählschleife die Zeile

#local Drehvektor=Drehvektor+ <0,40,0>;

durch

#local Drehvektor=Drehvektor+ <10,10,0>;

,so erhält man einen schönen Bewegungsablauf z.B. für eine Animation, da nun zwei Drehachsen miteinander kombiniert werden. Probiere es aus!

b) vaxis_rotate (A,B,F)

A ist dabei ein gegebener Punkt P(x,y,z), B ist der Vektor, durch den die gewünschte Drehachse dargestellt wird, F ist der Drehwinkel. In der ff. Abbildung (vgl. Skript per Mausklick) sind die Drehachsen rot, grün, blau und gelb dargestellt. Der Startpunkt A=P wird jeweils um eine dieser Achsen mit einem bestimmten Winkel gedreht.


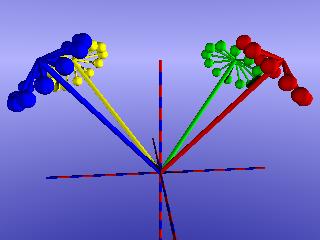So, aber dass es hier ohne Eigenprogrammierung abgeht, hast du eh nicht erwartet. Hier also die Aufgaben:

Aufgabe vekt_a:
Eine Kugel soll im Abstand 3 LE um die x-Achse rotieren.

Aufgabe vekt_b:
Eine Kugel soll im Abstand 4 LE um die z-Achse rotieren.

Aufgabe vekt_c:
Eine Kugel soll um eine Kombination zweier Achsen rotieren, ihre Farbe soll dabei vom Schleifenzähler abhängen.

Aufgabe vekt_d:
Eine Kugel soll um die Winkelhalbierendex von x-Achse und y-Achse rotieren.

Aufgabe vekt_e:
Zwei schön anzuschauende Bilder mit vrotate.

Aufgabe vekt_f:
Zwei schön anzuschauende Bilder mit vaxis_rotate

Und hier wieder die Beispiele zum Spicken:




Ja, das war der erste Teil, ich hoffe, das Programmieren hat euch auch Spaß gemacht, das Lernen hat die kleinen grauen Zellen angeregt und schöne Bilder hervorgebracht!

Noch Zeit übrig? Na, dann geht's weiter mit Teil 2!

• Zum Seitenanfang